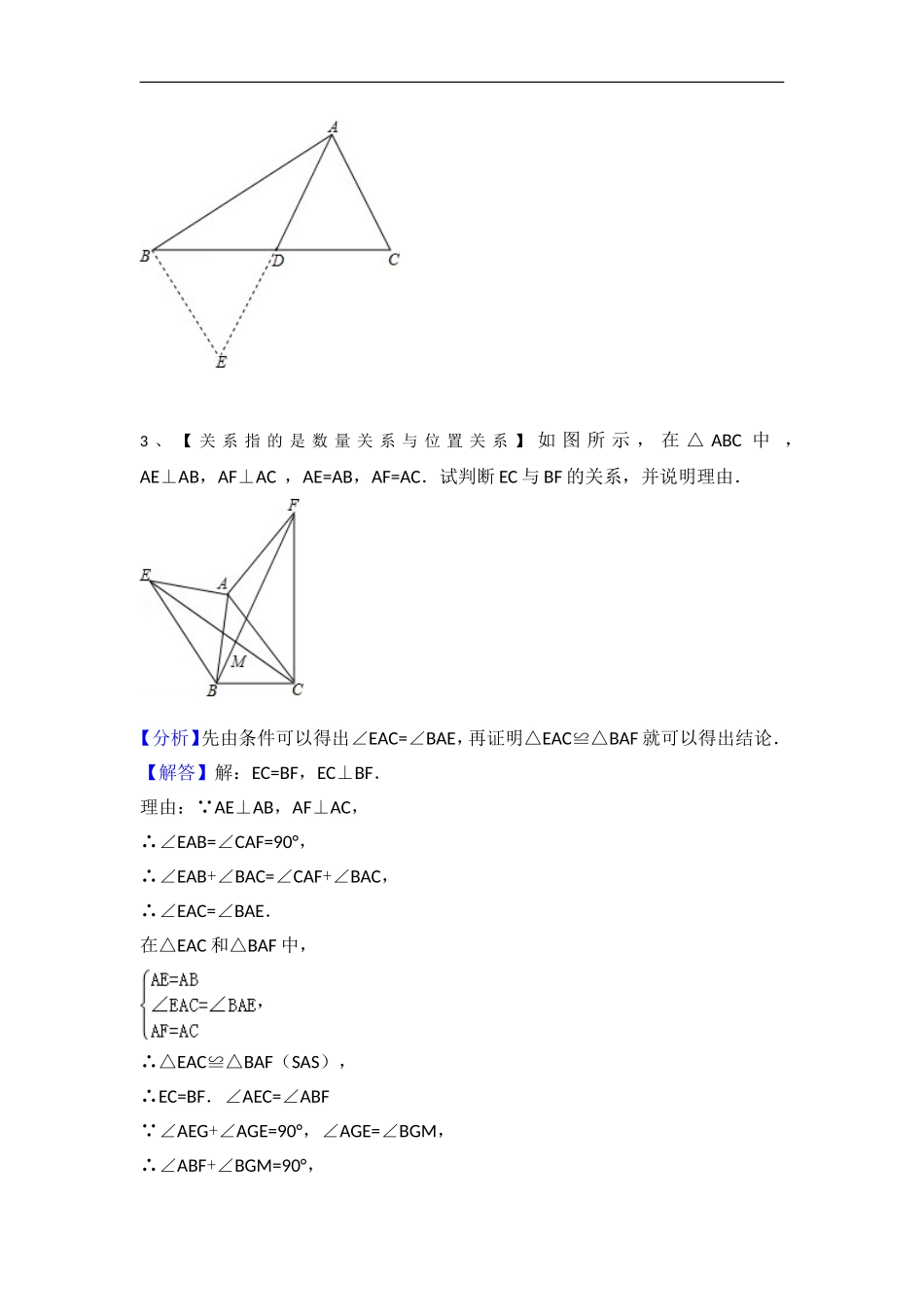
1、【截长补短】如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.【分析】在BC上找到F使得BF=BE,易证∠BOE=∠COD=60°,即可证明△BOE≌△BOF,可得∠BOF=∠BOE=60°,即可证明△OCF≌△OCD,可得CF=CD,根据BC=BF+CF即可解题.【解答】证明:在BC上找到F使得BF=BE, ∠A=60°,BD、CE是△ABC的角平分线,∴∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=120°,∴∠BOE=∠COD=60°,在△BOE和△BOF中,,∴△BOE≌△BOF,(SAS)∴∠BOF=∠BOE=60°,∴∠COF=∠BOC﹣∠BOF=60°,在△OCF和△OCD中,,∴△OCF≌△OCD(ASA),∴CF=CD, BC=BF+CF,∴BC=BE+CD.2、【加倍中线】如图,△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=5,AC=3,求AD的取值范围.【分析】(1)再延长AD至E,使DE=AD,构造△ADC≌△EDB,再根据三角形的三边关系可得AB+AC>2AD;(2)直接利用三角形的三边关系:三角形两边之和大于第三边,三角形的两边差小于第三边可得53﹣<2AD<5+3,再计算即可.【解答】(1)证明:由BD=CD,再延长AD至E,使DE=AD, D为BC的中点,∴DB=CD,在△ADC和△EDB中,∴△ADC≌△EDB(SAS),∴BE=AC,在△ABE中, AB+BE>AE,∴AB+AC>2AD;(2) AB=5,AC=3,∴53﹣<2AD<5+3,∴1<AD<4.3、【关系指的是数量关系与位置关系】如图所示,在△ABC中,AE⊥AB,AF⊥AC,AE=AB,AF=AC.试判断EC与BF的关系,并说明理由.【分析】先由条件可以得出∠EAC=∠BAE,再证明△EAC≌△BAF就可以得出结论.【解答】解:EC=BF,EC⊥BF.理由: AE⊥AB,AF⊥AC,∴∠EAB=∠CAF=90°,∴∠EAB+∠BAC=∠CAF+∠BAC,∴∠EAC=∠BAE.在△EAC和△BAF中,,∴△EAC≌△BAF(SAS),∴EC=BF.∠AEC=∠ABF ∠AEG+∠AGE=90°,∠AGE=∠BGM,∴∠ABF+∠BGM=90°,∴∠EMB=90°,∴EC⊥BF.4、已知,如图一,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.求证:(1)DE=BD+CE.(2)如图二,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,我们能猜想得到什么结论?(请直接写出结论)【分析】(1)只要证明△ACE≌△BAD(AAS),得到BD=AE,CE=AD,即可推出DE=AE+AD=BD+CE.(2)在图2的情况下:DE=CEBD﹣.证明方法类似.【解答】解:(1)在图1的情况下:DE=BD+CE证明: ∠DAB+∠EAC=90,∠DAB+∠DBA=90°,∴∠EAC=∠DBA,在△ADB和△CEA中,,∴△ACE≌△BAD(AAS),∴BD=AE,CE=AD,∴DE=AE+AD=BD+CE.(2)在图2的情况下:DE=CEBD﹣.理由:: ∠DAB+∠EAC=90,∠DAB+∠DBA=90°,∴∠EAC=∠DBA,在△ADB和△CEA中,,∴△ACE≌△BAD(AAS),∴BD=AE,CE=AD,∴DE=ADAE=CEBD﹣﹣.5、【同角的余角相等】如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.(1)求证:BD=BC;(2)若BD=6cm,求AC的长.【分析】(1)欲证明BD=BC,只要证明△ABC≌△EDB即可.(2)由E是BC中点,BD=6cm,BD=BC,推出BE=BC=BD=3cm,由△ABC≌△EDB,得到AC=BE,即可解决问题.【解答】(1)证明: DE⊥AB,∴∠BFE=90°,∴∠ABC+∠DEB=90°, ∠ACB=90°,∴∠ABC+∠A=90°,∴∠A=∠DEB,在△ABC和△EDB中,,∴△ABC≌△EDB,∴BD=BC.(2)解: E是BC中点,BD=6cm,BD=BC,∴BE=BC=BD=3cm, △ABC≌△EDB,∴AC=BE=3cm.6、【同角的余角相等】已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.【分析】根据余角的性质得到∠A=∠BDE,根据全等三角形的判定定理得到△ABC≌△BDF,由全等三角形的性质即可得到结论.【解答】证明: ∠ACB=∠FBD=∠90°, DE⊥AB,∴∠A+∠ABC=∠ABC+∠BDE=90°,∴∠A=∠BDE.在△ABC与△BDF中,,∴△ABC≌△BDF,∴AB=DF.7、【动点问题】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,...