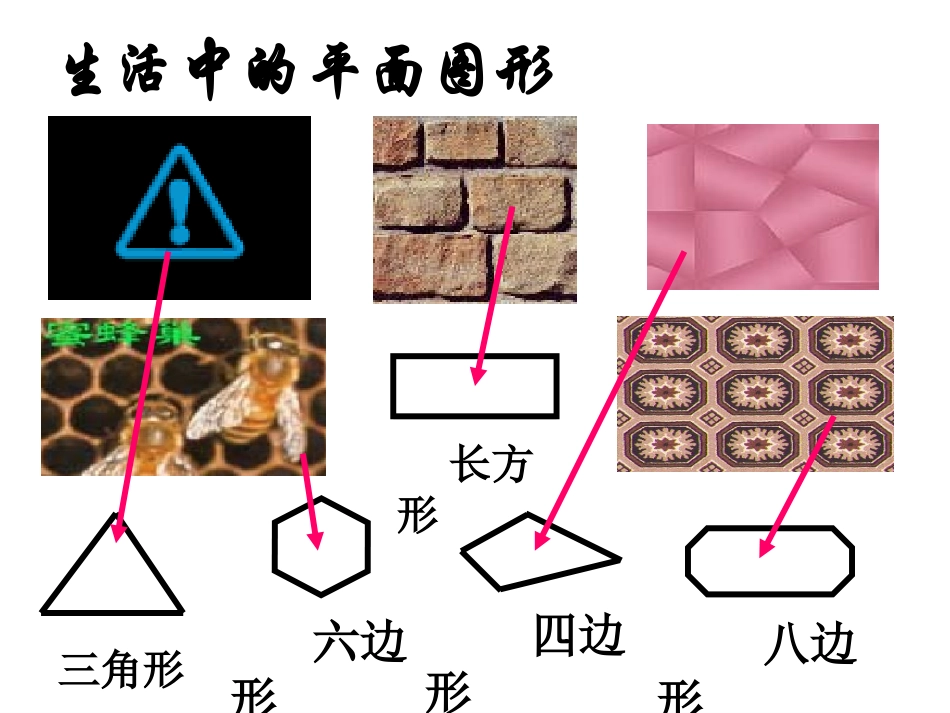
生活中的平面图形三角形长方形四边形六边形八边形边边内角内角顶点顶点定义定义::在平面内,由若干条不在同在平面内,由若干条不在同一条直线上的线段首尾顺次相连组一条直线上的线段首尾顺次相连组成的封闭图形叫做成的封闭图形叫做多边形多边形。。对角线对角线多边形的有关概念.DBAEC注:这里所说的多边形都是指凸多边形.思考:一个多边形至少有多少条边?多边形有几条边,就叫几边形有n条边的多边形叫n边形()3n过多边形任一顶点有多少条对角线?这些对角线将多边形分成多少个三角形?多边形三角形四边形五边形六边形…n边形对角线条数…三角形个数…01122334n-3n-2三角形六边形四边形探索多边形的内角和五边形180°360°540˚720˚发现:从n边形的一个顶点引出的对角线把n边形分成(n-2)个三角形.从而得出:n边形的内角和计算公式:(n-2)·180˚.这种探索方法你掌握了吗?请完成下表多边形的边数34567…n分成的三角形个数12…多边形的内角和180°360°…345n-2900°(n-2)×180˚720°540°n边形的内角和为:(n-2)×180°发现:多边形每增加一条边,则它的内角和的度数增加180˚.n边形的内角和为:(n-2)×180°n边形内角和定理:n边形内角和等于()02180n思考你还有别的方法求多边形内角和吗?ACDEFB六边形内角和:(6-2)·180°=4×180°=720°ACDEBFO六边形内角和:(6-1)·180-180°=(6-2)×180°=720°ACDEBFO六边形内角和:6×180°-360°=4×180°=720°以上三种求六边形内角和的方法,体现了数学的化归思想:化多边形问题为三角形问题来解.求多边形的内角和公式:(n-2)·180˚.也可利用以上三种方法推得.你能证明多边形的外角和是多少度吗?推论:任意多边形的外角和等于0360ABCDEF11、如图:、如图:((11)作多边形所有过顶点)作多边形所有过顶点AA的对角线,并分的对角线,并分别用字母表示出来。别用字母表示出来。((22)求这个多边形的内角和。)求这个多边形的内角和。解:对角线解:对角线ACAC、、ADAD、、AEAE;;解:解:44╳╳180°=720°180°=720°随堂练习随堂练习例1填空:1.十边形的内角和是________;2.(a+1)边形的内角和是________.3.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形是边形.它的内角和是度.1440°(a-1)·180°七900解:n-2=5n=7. ∴则(n-2)·180°=(7-2)·180˚=900˚答:这个多边形的内角和为900˚已知一个多边形,它的内角和等于720°,求这个多边形的边数。解:设多边形的边数为n,因为它的内角和等于(n-2)•180°,所以,(n-2)•180°=720º。解得:n=6这个多边形的边数为6。例2.已知一个多边形,它的内角和等于五边形内角和的2倍,求这个多边形的边数。解:设多边形的边数为n,因为它的内角和等于(n-2)•180°,五边形内角和等于540º,所以,(n-2)•180°=2×540º。解得:n=8这个多边形的边数8。例3.练习练习11、、nn边形的内角和等于边形的内角和等于____________________,九边形的内角和等于,九边形的内角和等于__________________________________________________。。22、一个多边形的内角和等于、一个多边形的内角和等于14414400°°,那么它是,那么它是____________边形。边形。(n-2)•180°(n-2)•180°(9-2)•180°(9-2)•180°=1260°=1260°十十44、从六边形的一个顶点出发可画、从六边形的一个顶点出发可画__________条对角线,这些对角线把六边条对角线,这些对角线把六边形分成形分成__________个三角形。个三角形。33、正五边形的每一个内角的度数、正五边形的每一个内角的度数是是______________。。108°108°三三四四小结小结11、什么是多边形?、什么是多边形?在平面内,由若干条不在平面内,由若干条不在同一条直线上的线段首尾在同一条直线上的线段首尾顺次相连组成的封闭图形叫顺次相连组成的封闭图形叫做做多边形多边形。。2.2.nn边形的内角和等于边形的内角和等于(n-2)(n-2)•180°.•180°.4.三种求多边形内角和的方法,体现了数学的化归思想:化多边形问题为三角形问题来解.3.3.过过nn边形的某一个顶点的边形的某一个顶点的所有对角线有几条?被分成所有对角...