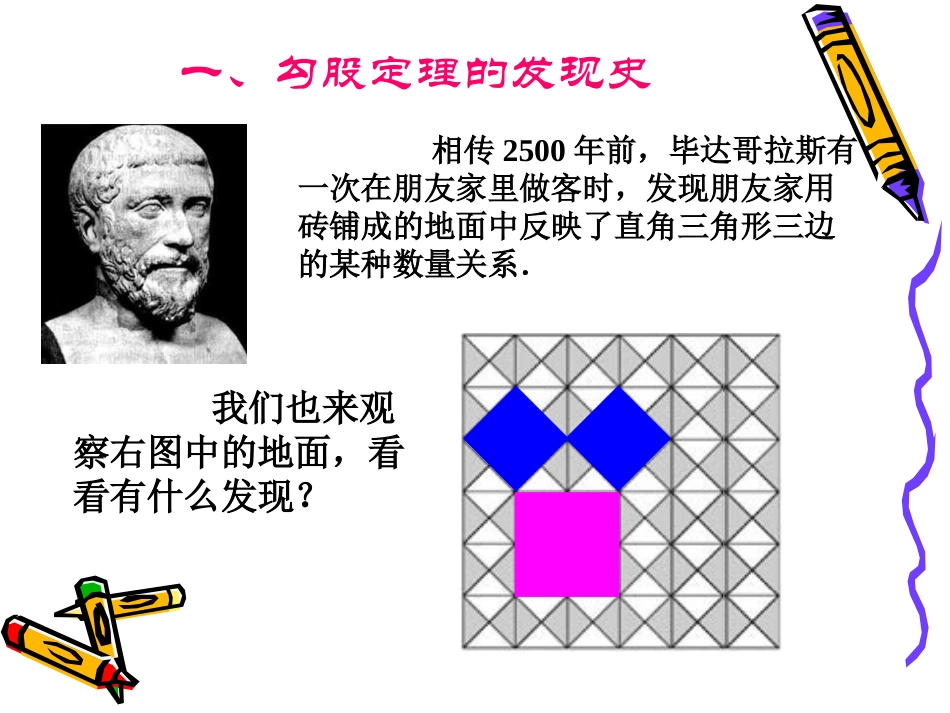
18.118.1勾股定理(勾股定理(11))人教版八年级数学(下)广元市利州区东城实验学校韩思春这就是本届大会会徽的图案.这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.引言:感知勾股定理感知勾股定理你见过这个图案吗?相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.我们也来观察右图中的地面,看看有什么发现?一、勾股定理的发现史面积A+面积B=面积Caa22+b+b22=c=c22两直角边的平方和等于斜边的平方abcABCABC网格中的直角三角形是否也具有这种性质?(网格中每个小方格的面积都是1)正方形A的面积正方形B的面积正方形C的面积16259二、直角三角形三边关系的再探索ABCacbSa+Sb=Sc设:直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c之间的关系?a2+b2=c2三、直角三角形三边关系的猜想┏acb如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。勾股弦命题1:四、命题证明的精彩再现abababab222cbaCCCC如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2直角三角形两直角边的平方和等于斜边的平方.acb勾股弦勾股定理(毕达哥拉斯定理)222222cabacbbca我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。目前世界上许多科学家正在试图寻找其它星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言,音乐,各种图形等.我国数学家华罗庚建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的.。.ABCD例1.已知:如图,等腰△ABC的周长是32cm,底边长是12cm。(1)求高AD的长;(2)求S△ABC五、勾股定理的运用比一比看看谁算得快!练习1.求下列直角三角形中未知边的长:8x171620x125x3.在一个直角三角形中,两边长分别为3、4,则第三边的长为________5或1.在等腰Rt△ABC中,a=b=1,则c=___2.在Rt△ABC中,∠A=30°,AB=2,则BC=___AC=___CAB第1题图第2题图√2√3√71abcCBA练习2.填空:在在Rt△ABDRt△ABD中,∠中,∠DABDAB==90º90º∴∴BDBD22==ADAD22++ABAB22==3322++4422==2525∴∴BDBD==55同理可得同理可得DCDC==1313解:解:已知:四边形已知:四边形ABCDABCD中,中,∠∠DABDAB=∠=∠DBCDBC==90º90ºADAD==33,,ABAB==44,,BCBC==1212求:求:DCDC的长。的长。例例22::BBCCDDAA练习3.如图1.1-1,求图中字母M所代表的正方形的面积.图1.1-1图1.1-2练习4.如图1.1-2,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.M7545FEDCBA例3、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?8m2m8mABCDE六、小结::七、布置作业:勾股定理从边的角度刻画了直角三勾股定理从边的角度刻画了直角三角形的又一个特征.角形的又一个特征.人类对勾股定理的研究已有近人类对勾股定理的研究已有近30003000年年的历史,在西方,勾股定理又被称为“毕的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥达哥拉斯定理”、“百牛定理”、“驴桥定理”等等.定理”等等.必做必做p69—701p69—701、、22、、33、、44题题选做选做p71p71阅读与思考阅读与思考(分层次布置作业,使学生在原有的基础上(分层次布置作业,使学生在原有的基础上都能得到提高。)都能得到提高。)再见