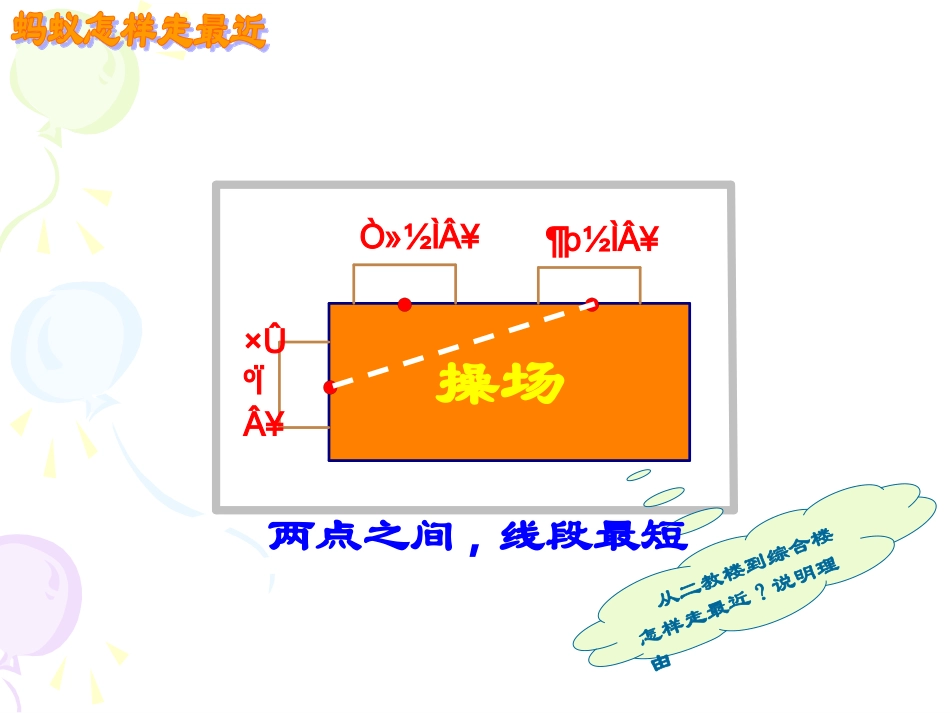
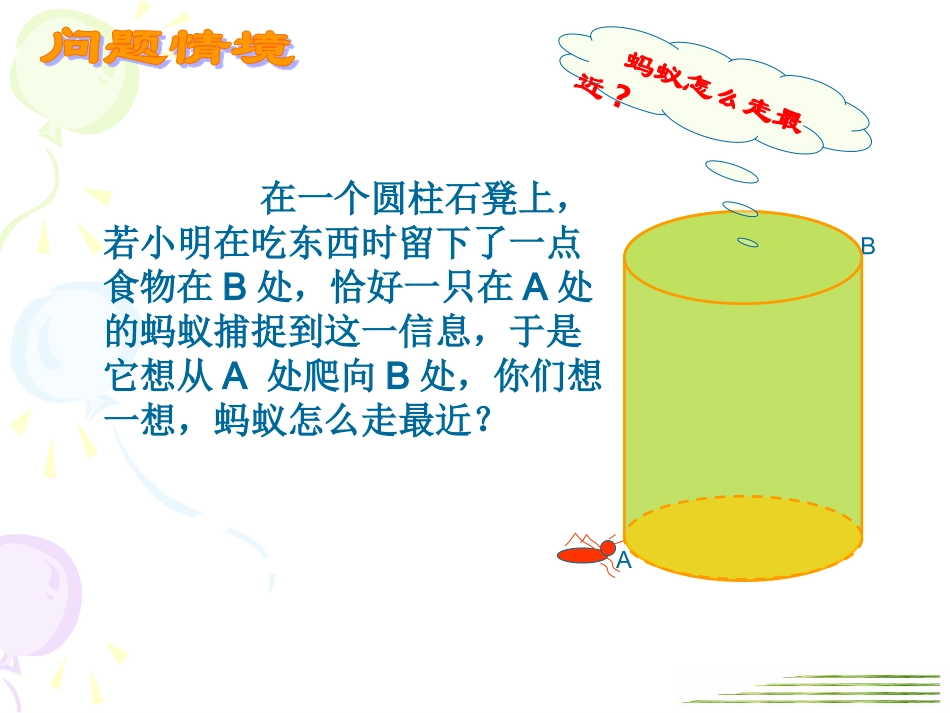
操场石室联中平面图×ÛºÏÂ¥¶þ½ÌÂ¥Ò»½ÌÂ¥从二教楼到综合楼怎样走最近?说明理由两点之间,线段最短BA蚂蚁怎么走最近?在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,你们想一想,蚂蚁怎么走最近?BA以前后两桌4人为一组,研究蚂蚁爬行的最短路线蚂蚁A→B的路线BAA’dABA’ABBAO下一页>>ABA’BAA’rOh怎样计算AB?在Rt△AA’B中,利用勾股定理可得,222'BAAAAB侧面展开图其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)若已知圆柱体高为12cm,底面半径为3cm,π取3,则:15)33(12222ABABBAA’3O12侧面展开图123πAA’B你学会了吗?小试牛刀练习1练习2练习31.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?±±¶«CBA解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:AB=2×6=12(千米)AC=1×5=5(千米)在Rt△ABC中22222213169125ABACBC∴BC=13(千米)即甲乙两人相距13千米小试牛刀练习1练习2练习32.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离。3220BA2222256252015AB小试牛刀练习1练习2练习33.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?你能画出示意图吗?解:设伸入油桶中的长度为x米,则最长时:5.225.1222xx最短时:∴最长是2.5+0.5=3(米)5.1x答:这根铁棒的长应在2-3米之间∴最短是1.5+0.5=2(米)1.如图,在棱长为10cm的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1cm/s,且速度保持不变,问蚂蚁能否在20s内从A爬到B?B食物A举一反三BAB两条线路,看明白了吗?举一反三1.如图,在棱长为10cm的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1cm/s,且速度保持不变,问蚂蚁能否在20s内从A爬到B?举一反三中国古代人民的聪明才智真是令人赞叹!在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?举一反三解:设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得:BC2+AC2=AB2即52+x2=(x+1)225+x2=x2+2x+1,2x=24,∴x=12,x+1=13答:水池的水深12尺,这根芦苇长13尺。小结运用勾股定理解决实际问题时,应注意:1、没有图的要按题意画好图并标上字母;2、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。课后作业2*.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?1.课本习题1.5第1,2,3题。