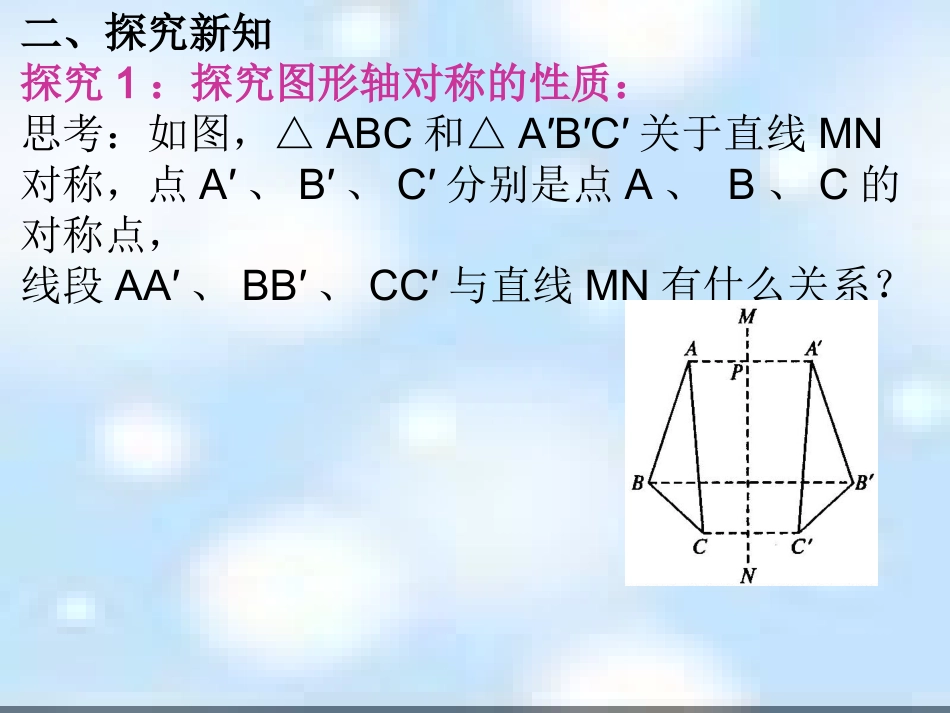
19.1轴对称(3)一.复习旧知1、轴对称图形定义二、探究新知探究1:探究图形轴对称的性质:思考:如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?线段的垂直平分线定义:经过线段_____并且______于这条线段的_____,叫做这条线段的垂直平分线.图形轴对称的性质•(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的________.•(2)轴对称图形的对称轴是任何一对对称点所连线段的__________.lAA’BB’CC’----------------------------------如图:l垂直平分————,l垂直平分————,l垂直平分————.探究2::探究线段垂直平分线的性质.问题:如下图.木条L与AB钉在一起,L垂直平分AB,P1,P2,P3…,是L上的点,分别量一量点P1,P2,P3…,到A与B的距离,你有什么发现?AP1____BP1,AP2_______BP2…,结论:线段垂直平分线上的点与这条线段两个_____的____相等.已知:____________________求证:____________________线段的垂直平分线的性质定理:线段的垂直平分线上的点到这条线段的两个端点的距离相等.几何语言:∵点P在线段AB的垂直平分线上∴PA=PBNABPM∵MNAB⊥于C,AC=CB,点P在MN上∴PA=PB或归纳1CBACDDABCPEDABCACDB1.如图:若AC垂直平分BD,则AB=_____2.如图:若BD垂直平分AC,则AB=______3.如图:若AC、BD互相垂直平分,则AB=________4.如图:PD、PE分别垂直平分线段AB、BC,则PA___PC(1)辨析练习:(2)(3)(4)ADBCBC=CB=DA=基础闯关如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED=cm;如果∠ECD=600,那么∠EDC=0.EDABC760三、巩固训练1、如图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长=()2、如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。NMCBA3、如图,ADBC⊥,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB、BD与DE三条线段之间有什么关系?五、小结本堂课你学到了什么?