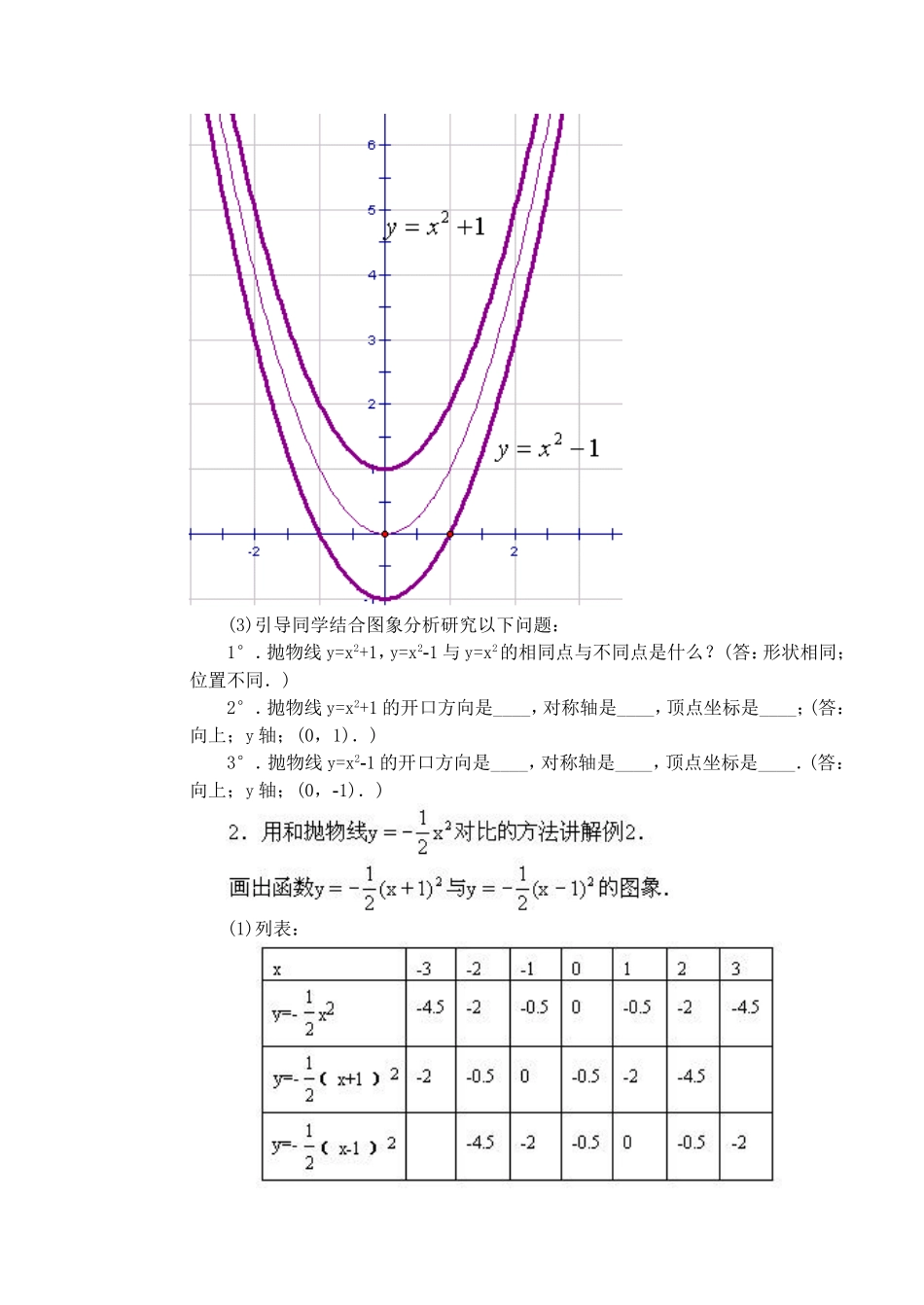
二次函数y=ax2+bx+c的图象(一)一、教学目的1.使学生会用描点法画出二次函数y=ax2+k型与y=a(x-h)2型的图象.2.使学生了解并会求抛物线y=ax2+k与y=a(x-h)2的对称轴与顶点.二、教学重点、难点重点:1.用描点法画出二次函数y=ax2+k型与y=a(x-h)2型的图象.2.二次函数y=ax2+k,y=a(x-h)2与y=ax2的联系.难点:1.二次函数y=ax2+k,y=a(x-h)2与y=ax2的联系.2.对于抛物线y=ax2+k,y=a(x-h)2的对称轴方程的理解.三、教学过程复习提问1.用描点法画出函数y=x2的图象,并根据图象回答下列问题:(1)抛物线y=x2的开口方向、对称轴与顶点坐标;(2)当x=-2时,y的值;(3)当y=9时,x的值.(2)当x=-3时,y的值(精确到0.1);(3)当y=-9时,x的值(精确到0.1).新课1.用和抛物线y=x2对比的方法讲解例1.画出函数y=x2+1与y=x2-1的图象.(1)列表:x-3-2-10123y=x29410149y=x2+1105212510y=x2-1830-1038(2)在同一平面直角坐标系中画出图象;(3)引导同学结合图象分析研究以下问题:1°.抛物线y=x2+1,y=x2-1与y=x2的相同点与不同点是什么?(答:形状相同;位置不同.)2°.抛物线y=x2+1的开口方向是____,对称轴是____,顶点坐标是____;(答:向上;y轴;(0,1).)3°.抛物线y=x2-1的开口方向是____,对称轴是____,顶点坐标是____.(答:向上;y轴;(0,-1).)(1)列表:(2)在同一平面直角坐标系中画出图象;(3)引导同学结合图象分析研究以下问题:什么?(答:形状相同;位置不同.)(答:向下;x=-1;(-1,0).)____.(答:向下;x=1;(1,0).)小结用填空或列表的方法总结抛物线y=ax2,y=ax2+k,y=a(x-h)2,y=a(x+h)2的开口方向、对称轴、顶点坐标.1.当a>0时,抛物线y=ax2的开口方向是____,对称轴是____,顶点坐标是____;y=ax2+k的开口方向是____,对称轴是____,顶点坐标是____;y=a(x-h)2的开口方向是____,对称轴是____,顶点坐标是____;y=a(x+h)2的开口方向是____,对称轴是____,顶点坐标是____.2.当a<0时,抛物线y=ax2的开口方向是____,对称轴是____,顶点坐标是____;y=ax2+k的开口方向是____,对称轴是____,顶点坐标是____;y=a(x-h)2的开口方向是____,对称轴是____,顶点坐标是____;y=a(x+h)2的开口方向是____,对称轴是____,顶点坐标是____.四、教学注意问题1.用“抽象→具体→抽象”的思考方法突破教学难点.位置沿x轴方向平移,学生不易理解,此时可结合函数对应值表,用具体的数字说明.2.用联想的方法突破教学难点.3.充分运用对比分析法.4.注意培养学生观察图象分析问题的能力.5.注意渗透分类讨论思想,培养学生数学思维的周密性.