直线与双曲线VIP免费

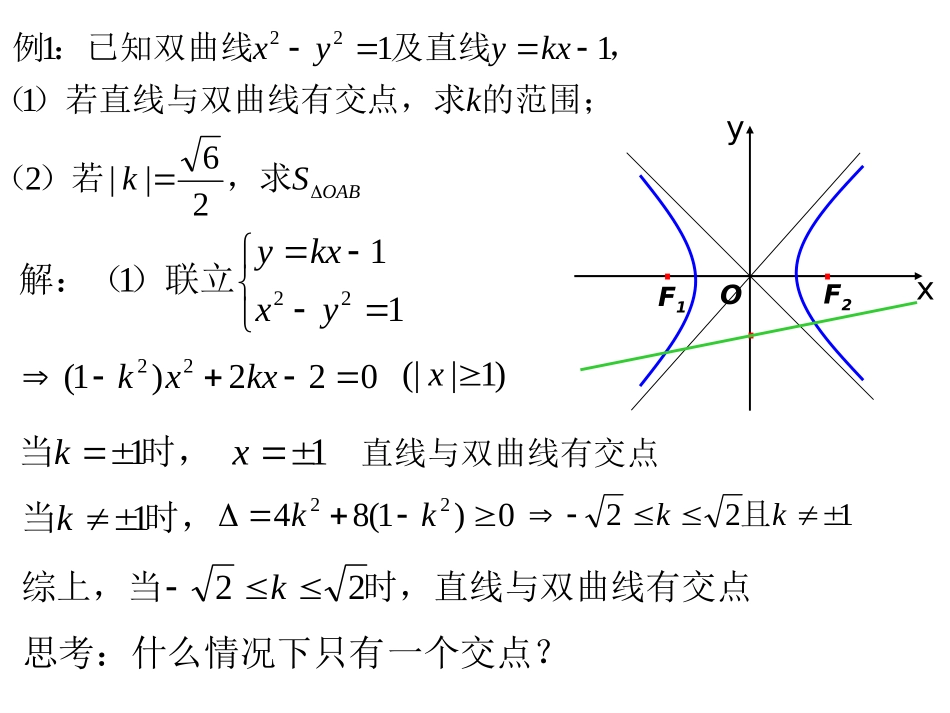
直线与双曲线直线与椭圆：（2）弦长问题||1||2akAB（3）弦中点问题（4）经过焦点的弦的问题（1）直线与椭圆位置关系韦达定理或设点作差法0___||)1(1||//2akABOABSkkkxyyx，求）若（的范围；点，求）若直线与双曲线有交（，及直线：已知双曲线例26||2111122y..F2F1O.x11122yxkxy）联立解：（022)1(22kxxk)1|(|x时，当1k1x直线与双曲线有交点时，当1k0)1(8422kk122kk且点时，直线与双曲线有交综上，当22k一个交点？思考：什么情况下只有OABSkkkxyyx，求）若的范围；（点，求）若直线与双曲线有交（，及直线：已知双曲线例26||2111122y..F2F1O.一个交点？思考：什么情况下只有点直线与双曲线只有一交时，或当12kk交点？思考：什么情况下两个个交点时，直线与双曲线有两且当122kk交点在右支？思考：什么情况下两个个交点都在右支时，直线与双曲线有两当21k交点在两支上？思考：什么情况下两个个交点在两支上时，直线与双曲线有两当11k022)1(22kxxkOABSkkkxyyx，求）若（的范围；点，求）若直线与双曲线有交（，及直线：已知双曲线例26||2111122y..F2F1OAB)(,||21)2(的距离到直线是ABOddABSOAB211kd1122yxkxy联立022)1(22kxxk||1||2akAB由弦长公式：|1|481222kkk222211122121kkkkS21222kk12422yx已知双曲线方程：2例说明理由。的方程，若不存在，请求出直线，若存在，被双曲线所截弦的中点为，，使）是否存在直线（的方程；求直线的中点，为弦两点，若、）的直线交双曲线于，（）过（llNlABABMBAM2112111解：，则，，，设)()(2211yxByxA1242121yx1242222yx相减2121212121yyxxxxyyMMAByxk2121，即21ABk的方程为：直线AB)1(211xy.012yx即)(21xxxyo2222..NM12422yx已知双曲线方程：2例说明理由。的方程，若不存在，请求出直线，若存在，被双曲线所截弦的中点为，，使）是否存在直线（的方程；求直线的中点，为弦两点，若、）的直线交双曲线于，（）过（llNlABABMBAM2112111解法二：)1(1:xkylAB设，21k的方程为：直线AB)1(211xy.012yx即xyo2222..NM42122yxkkxy联立04)1(2)1(4)21(222kxkkxk121)1(22221kkkxx12422yx已知双曲线方程：2例说明理由。的方程，若不存在，请求出直线，若存在，被双曲线所截弦的中点为，，使）是否存在直线（llNl2112，则，，，的直线交双曲线于假设过)()()2(2211yxDyxCN1242121yx1242222yx相减2121212121yyxxxxyyNNyx211，即1CDkxy22：双曲线的渐近线方程为22CDkxyo2222..NM与双曲线没有交点直线l.)211(在为弦的中点的直线不存，以N。的垂直平分线必过定点）求证（；）求（的距离成等差数列。），（）且与点，（，的一支上有不同的三点在双曲线ACyyFyxCByxAxy2150),626(),,(1131231331122解：得由双曲线1131222xy.)50(是此双曲线的一焦点，点F三点在双曲线上支上，、、）由题意（CBA1由双曲线第二定义得：edAFAedAFA||edCFedBFCB，同理成等差数列、、CFBFAF.1231yy3例成等差数列CBAddd,,)()()(2222caycaycayCAB即y..F2F1OxCBA。的垂直平分线必过定点）求证（；）求（的距离成等差数列。），（）且与点，（，的一支上有不同的三点在双曲线ACyyFyxCByxAxy2150),626(),,(11312313311223例y..F2F1OxCBA)6,(20xAC的中点坐标为）设（11312113122222xyxy313131311312yyxxxxyy:相减1320xkAC)(213600xxxyAC的中垂线方程为：02252130yxx即.2250），（此直线过定点的范围。对称的两点，求线，双曲线上存在关于直已知双曲线kkxylyx4:13.222的双曲线方程。弦长为所截得的，且直线：求渐进线方程为33803021yxyx作业：