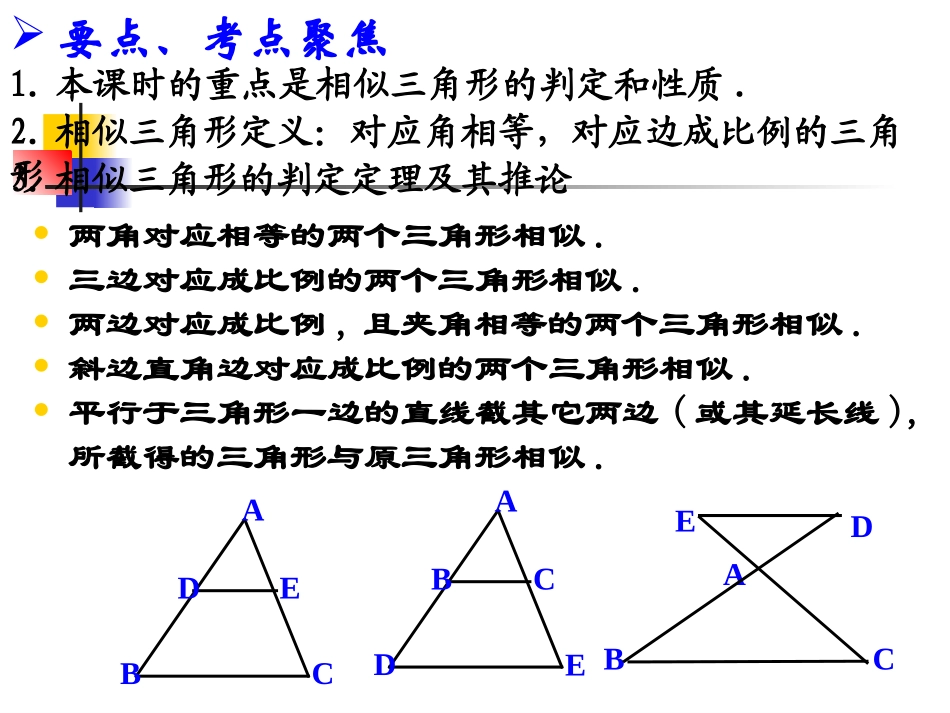
要点、考点聚焦1.本课时的重点是相似三角形的判定和性质.2.相似三角形定义:对应角相等,对应边成比例的三角形.3.相似三角形的判定定理及其推论两角对应相等的两个三角形相似.三边对应成比例的两个三角形相似.两边对应成比例,且夹角相等的两个三角形相似.斜边直角边对应成比例的两个三角形相似.平行于三角形一边的直线截其它两边(或其延长线),所截得的三角形与原三角形相似.ABCDEADEBCEDCBA4.相似三角形的性质(1)相似三角形对应角相等,对应边成比例.(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.(3)相似三角形周长的比等于相似比.推论:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.要点、考点聚焦相似多边形周长的比等于,对应对角线的比等于,对应三角形相似,且相似比等于,对应三角形面积的比等于;相似多边形面积的比等于.相似比相似比相似多边形的相似比相似比的平方相似比的平方课前热身2.如图所示,在平行四边形ABCD中,G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有()A.3对B.4对C.5对D.6对1.下列命题正确的是()A.所有的直角三角形都相似B.所有的等腰三角形都相似C.所有的等腰直角三角形都相似D.以上结论都不正确CC3.若如图所示,△ABC∽△ADB,那么下列关系成立的是()A.∠ADB=∠ACBB.∠ADB=∠ABCC.∠CDB=∠CABD.∠ABD=∠BDC4.△ABC中,AC=6,BC=4,CA=9,△ABC∽△A′B′C′,△A′B′C′最短为12,则它的最长边的长度为()A.16B.18C.27D.24BC课前热身5.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有_____条.课前热身在通往光明中学的路上有一铁路岔口,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点将升高多少m?1m16moBDCA┏┛0.5m8m问题1在光明中学的附近有一个池塘,为了测量池塘的宽AB,有人在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=40m,DC=30m,DE=30m,那么你能算出池塘的宽AB吗?ABCDE问题2AB=70mAEBFDC1.如图,在ABCD中,E是BC上一点,BE:EC=1:2,AE与BD相交于F,则BF:FD=_______,SADF△:SEBF△=______1:39:1问题3一进入光明中学的校门,便发现校门口的板报上有一块<数学园地>,上面有二道题目:2.如图,矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,判断下列两个结论是否成立?若成立,请证明.若不成立,请说明理由.①△AEFCEA∽△②∠AFE+ACE=45°∠.GABCDEFH问题4光明中学有一家校办工厂,该厂为了应对激烈的市场竞争,提高原材料的利用率,减少浪费,计划将一种三角形铁皮余料加工成矩形铁皮,相关的信息和加工要求如下:(1)已知这种三角形余料的底边BC=160cm,高AD=120cm(2)要求截出来的矩形的一边在BC上如果按照上述要求,将这种三角形铁皮余料加工成面积尽可能大的矩形铁皮,你能设计出符合要求的加工方案吗?如果能,请求出这个最大面积及相应矩形的两邻边之长。ADBCGEHFM如果要求以截取出来的面积最大的矩形铁皮为侧面,围成一个体积尽可能大的圆柱形铁桶,你认为该怎样围呢?请说明理由。(注:围铁桶侧面时,接缝无重叠,底面另用材料配备)ADBCGEHFM问题5一块直角三角形的铁皮材料,两直角边长分别是30cm、40cm,现要把它加工成一个面积最大的正方形,两种加工方法如下图,请用学过的知识说明哪种加工方法符合要求?ABCEDFABCDEFGP问题6在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB于点E,点F在AC上,DC=DF,若BC=3,BE=4,CD=x,CF=y,求y于x的函数关系式,并写出自变量x的取值范围。ABCDEF小胖和小瘦在公园玩标准的跷跷板游戏,小胖对小瘦说:真可惜!我现在最高只能把你翘到1米高,如果我俩各边都伸长相同的一段长度,那么我能将你翘到1.25米,甚至更高!(1)你认为小胖的话对吗?请你作图分析说明;(2)你能否找到将小瘦翘到1.25米高的方法?试说明.问题6OBAOABPCBACPOA1C11.在某时刻的阳光照耀下,身高160cm的小红的影长为80cm,她身旁的旗杆影长10m,则旗杆高为___m.2.已知,某建筑物形状如图所示,该建筑物分商贸城和住宅区两部分,设计AB=120m,AE=60m...