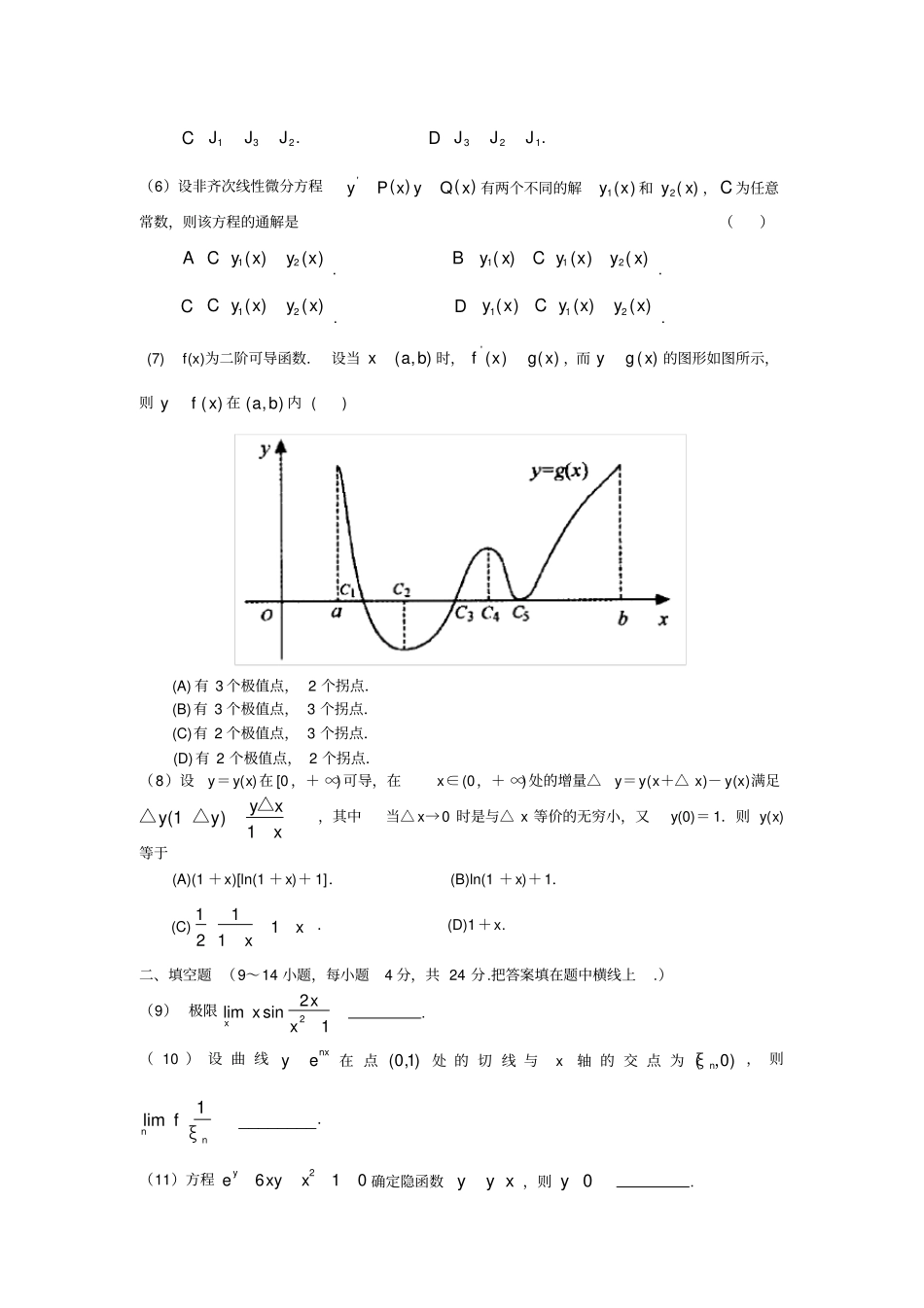
考研数学高数部分模拟题时间180分钟满分150分姓名分数一、选择题(1~8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内.)(1)设函数()fx在区间[-1,1]上连续,则0x是函数0()()xftdtgxx的()A跳跃间断点.B可去间断点.C无穷间断点.D震荡间断点.(2)曲线1ln(1)xyex,渐近线的条数为()A0.B1.C2.D3.(3)设函数fx在闭区间,ab上有定义,在开区间,ab内可导,则()A当0fafb时,存在,ab,使0f.B对任何,ab,有lim0xfxf.C当fafb时,存在,ab,使0f.D存在,ab,使fbfafba.(4)设24(,),xyfxye则()A''(0,0)(0,0)xyff存在,存在.B''(0,0)(0,0)xyff存在,不存在.C''(0,0)(0,0)xyff不存在,存在.D''(0,0)(0,0)xyff不存在,不存在.(5)22,1,2,3,ixyiDJedxdyi其中2221,DxyxyR,2222,2DxyxyR,3,,DxyxRyR,则123,,JJJ之间的大小顺序为()A123.JJJB231.JJJC132.JJJD321.JJJ(6)设非齐次线性微分方程)()('xQyxPy有两个不同的解)(1xy和)(2xy,C为任意常数,则该方程的通解是()A12()()Cyxyx.B112()()()yxCyxyx.C12()()Cyxyx.D112()()()yxCyxyx.(7)f(x)为二阶可导函数.设当),(bax时,)()('xgxf,而)(xgy的图形如图所示,则)(xfy在),(ba内()(A)有3个极值点,2个拐点.(B)有3个极值点,3个拐点.(C)有2个极值点,3个拐点.(D)有2个极值点,2个拐点.(8)设y=y(x)在[0,+∞)可导,在x∈(0,+∞)处的增量△y=y(x+△x)-y(x)满足xxyyy1)1(△△△,其中当△x→0时是与△x等价的无穷小,又y(0)=1.则y(x)等于(A)(1+x)[ln(1+x)+1].(B)ln(1+x)+1.(C)xx11121.(D)1+x.二、填空题(9~14小题,每小题4分,共24分.把答案填在题中横线上.)(9)极限22limsin1xxxx.(10)设曲线nxye在点)1,0(处的切线与x轴的交点为)0(,ξn,则________1limnnfξ.(11)方程2610yexyx确定隐函数yyx,则0y.(12)已知方程09623kxxx有且只有一个正根,则实数k的取值范围是__________.(13)交换积分次序1002111022._____d,dd,dyyxyxfyxyxfyI(14))(xf满足0)0(f,2)0('f,则._______cos1sinddlim000xxuttufxux三、解答题(15~23小题,共94分.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分10分)设.102,πcos12<2,322xxxxxxf试求38d2xxfI.(16)(本题满分11分)设,Fx在有一阶连续导数,且00f,并存在0f.若,00,0fxxFxxfx求Fx,并证明Fx在,连续。(17)(本题满分10分)设()fx是连续函数,(I)利用定义证明函数0()()xFxftdt可导,且()()Fxfx;(II)当()fx是以2为周期的周期函数时,证明函数200()2()()xGxftdtxftdt也是以2为周期的周期函数.(18)(本题满分11分)求二元函数22(,)2lnfxyxyyy的极值。(19)(本题满分10分)计算二重积分2ddDyxyxy,其中D是由直线,1,0yxyx所围成的平面区域.(20)(本题满分10分)设1,ab求证:函数xxxf2ln)(满足不等式.)(2122)()(02abbafbfaf(21)(本题满分10分)求微分方程562xyyye的通解.(22)(本题满分11分)设f(x)在[a,b]上连续,在(a,b)上可导,且f(a)=f(b)=1,证明:必存在ξ,η∈(a,b)使得1ef'f.(23)(本题满分11分)设D是位于曲线2(1,0)xayxaax下方、x轴上方的无界区域。(I)求区域D绕x轴旋转一周所成旋转体的体积V(a);(II)当a为何值时,V(a)最小?并求此最小值.一、1.B2.D3.C4.B5.A二、1【答案】0.【详解】把方程两边分别对x求导数得6620yeyyxyx当x=0时,从原方程得y=0,所以0y0.2.a=0,b=13.04.-2/35.1212e三、1.解:2300sinsinsinsinsinsin(sin)limlim2(1cos)xxxxxxxxxx2222000coscos(sin)cos1cos(sin)sin12lim2limlim3333xxxxxxxxxxx2.3.4.证令2()(1)()Fxxfx,则2()2(1)()(1)()Fxxfxxfx,由积分中值定理知,存在[3,4]c,使得4223(2)(1)()(1)()fxfxdxcfc,即(2)()FFc,由罗尔定理知,存在(2,)(2,4)c,使得()0F,即22(1)()(1)()0ff,即2()()1ff.5.证明:由212(1)11nnnnxxxx知{}nx有界,又由222122(1)0nnnnnnnxxxxxxx知{}nx单调递增故{}nx收敛,即nnxlim存在设limnnxl,12nnnxxx两边取极限得(2)lll,解之得0l或1l,又{}nx单调递增,故0l不合题意,舍去,因此lim1nnx6.7.设函数()yx在闭区间]1,1[上具有三阶连续导数,且,0)0(,1)1(,0)1(fff证明:在开区间)1,1(内至少存在一点,()3.f使解:方法一:在0()xfx处,将按泰勒公式展开,得2311()(0)(0)()(),2!3!fxffxfxxfx其中介于0与x之间,[1,1]x分别令11,xx和并结合已知条件,得11110(1)(0)(0)(),(10),26ffff22111(1)(0)(0)(),(11),26ffff两式相减,得12()()6ff由()fx的连续性,知()fx在闭区间在[12,]上有最大值和最小值,设它们分别为M、m.则有121[()()]2mffM再由连续函数的介值定理知至少存在一点12[,](1,1)121()[()()]32fff