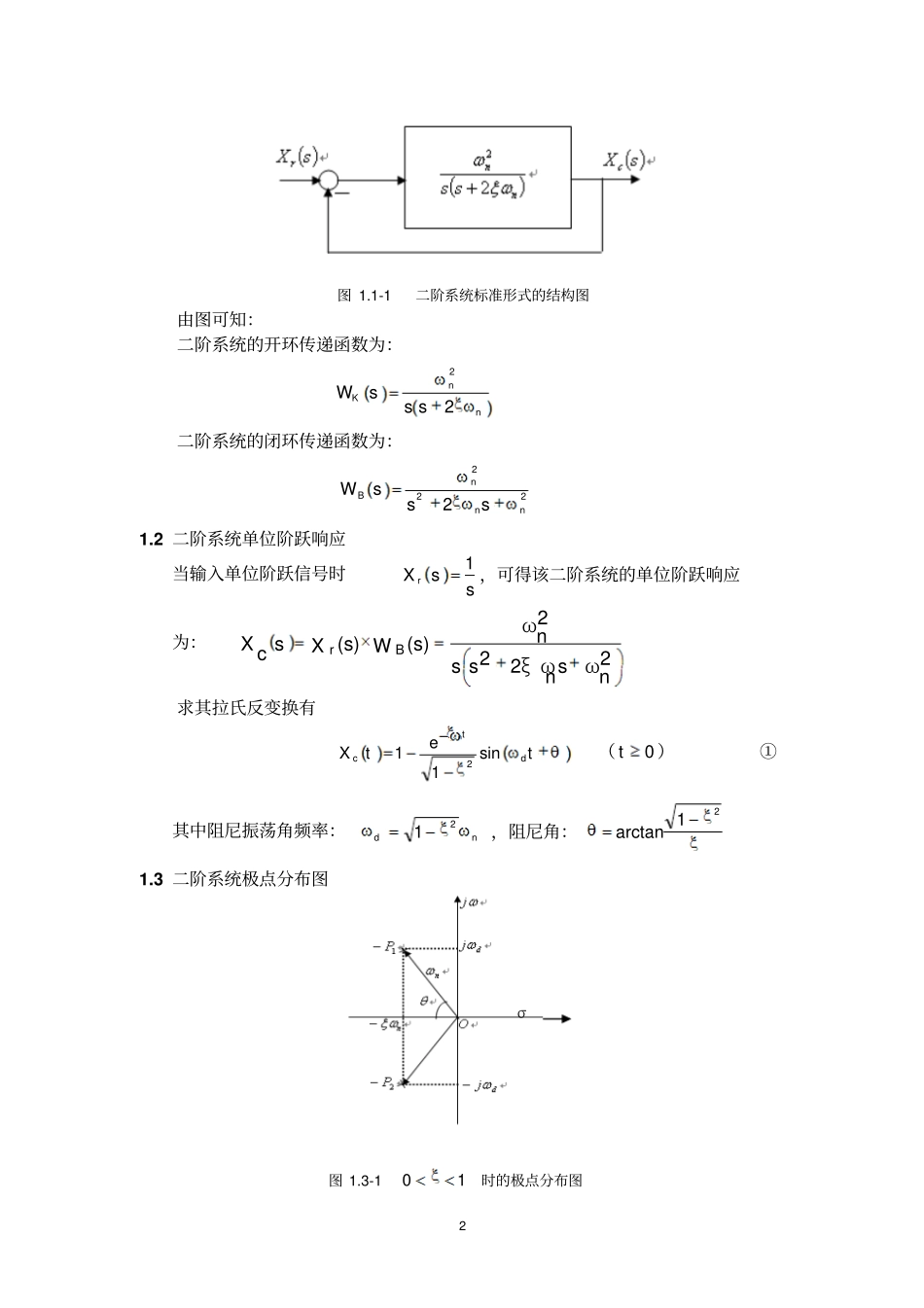
1闭环零点对二阶系统暂态的影响作者:智世宁班级:10电本2班学号:4100208211摘要二阶系统的单位阶跃响应是典型的二阶系统。因此分析二阶系统的单位阶跃响应,对于研究自动控制系统的暂态特性具有重要意义。在实际工作中,在一定的条件下,常常需要把一个高阶系统降为二阶系统来处理,这样的近似处理可以大大简化分析方法,减少计算量,而且任然不失其运动过程的基本性质。二阶系统在欠阻尼时的响应虽有振荡,但阻尼比ξ取值恰当,则系统既有响应的快速性,又有过渡过程的平稳性,因此在控制过程中常把二阶系统设计为欠阻尼的情况。大多数高阶系统中含有一对闭环主导极点,则该系统的动态响应就可以近似的用这对主导极点所描述的二阶系统来表达。本论文是通过直接求解系统在单位阶跃信号作用下的时域响应来分析系统的性能的。通过对设零点系统与未设零点系统上升时间、峰值时间、最大超调量、调节时间等暂态特性各个方面的对比,以及零点位置的变化对各动态性能变化趋势最终找到闭环零点对实际二阶系统的作用效果。关键字:暂态响应动态指标单位阶跃二阶系统欠阻尼闭环零点0引言由二阶微分方程描述的系统,称为二阶系统。欠阻尼振荡的二阶系统在实际中可以看成是稳定的系统,因此分析欠阻尼系统具有实际意义。二阶系统的单位阶跃响应是反映二阶系统本质的重要表现形式。我们在实际生产过程中,二阶系统总是需要满足工程最佳参数的要求,但是通过改变开环放大系数的方法可能会增大系统稳态误差。因此需要通过设置零点的方法从而达到既满足工程所需的阻尼比,又保证系统稳态精度的目的。正是由于闭环零点对二阶系统如此重要,所以此文主要分析闭环零点对二阶系统单位阶跃响应的影响。1二阶系统的描述一个系统的阶次是由其最简闭环传递函数分母S的最高次项的幂决定的。而二阶系统就是以2为S的最高次幂的闭环传递函数所对应的系统典型。简单来说,由二阶微分方程所描述的系统就叫做二阶系统。1.1二阶系统结构图及传递函数2图1.1-1二阶系统标准形式的结构图由图可知:二阶系统的开环传递函数为:nnKsssW22二阶系统的闭环传递函数为:2222nnnBsssW1.2二阶系统单位阶跃响应当输入单位阶跃信号时ssXr1,可得该二阶系统的单位阶跃响应为:2222nωsnξωssnω(s)W(s)XscXBr求其拉氏反变换有tetXdtcnsin112(0t)①其中阻尼振荡角频率:nd21,阻尼角:21arctan1.3二阶系统极点分布图图1.3-110时的极点分布图σ31.4二阶系统动态特性1.4.1上升时间rt(系统输出量第一次达到稳态值时所用的时间)令①中rtt时1tXc得0sin12rdttern在系统没有达到最后的稳定以前,为满足上式,使0)sin(trd得ndrt21②1.4.2峰值时间mt(系统输出量第一次达到最大值时所用的时间)令①中0dttdxc则第一个峰值对应的时间ndmt21③1.4.3最大超调量%(发生在第一个周期的峰值时间处)由于%100%cccmXXX且在单位阶跃输入下,稳定值1cX因此得%10021%e④1.4.4调节时间st()(txc与稳态值)(xc之间的偏差达到允许范围而不再超出的动态过程时间)nst3%5(9.00)nst4%2(9.00)⑤2具有零点的二阶系统的动态分析42.1具有零点的二阶系统结构图及传递函数图2.1-1带零点的二阶系统结构图具有零点的二阶系统的闭环传递函数为:)2(1)1(2)1()()()(222222nnnnnnBwswsswwswsswsXrsXcsWξττξτ其中τ为时间常数。令τ1=z,则上式可写为如下形式:)2()()()(222nnnwswszzswsXrsXcξ⑥由式⑥可得,该系统的闭环传递函数具有零点zs,将式⑥分解,由2222)()(1nnnwswssXrwsXcξ得)(11)(sXczsXcsXc2.2具有零点的二阶系统的单位阶跃响应为求其阶跃响应,设ssXr1)(,取初始条件为零,则Xc1(s)和Xc(s)的拉氏反变换为])2([)(22211nnncwswsswtxξdttdxztxsXcsXczstxccc)(1)()](1[)](1[)(1111⑦求出⑦中两项然后相加即得输出量,经过运算得)1cos(1)1sin(11)(2222θξξθξζξξtwwltwlwzzletxnnnntwcn⑧上述式子中的“l”为极点与零点间的距离,在复平面上画出其位置(假设零点在极点左侧))2()(222nnnwswszzswξ)(sXr)(sXc5由上图可知:φξφξξξsin1cos)1()(22221lwlwzwwzpzlnnnn故式子⑧可以写成:θφξξξtwzletxntwcn221sin11)(⑨式子中:ξξθ21...