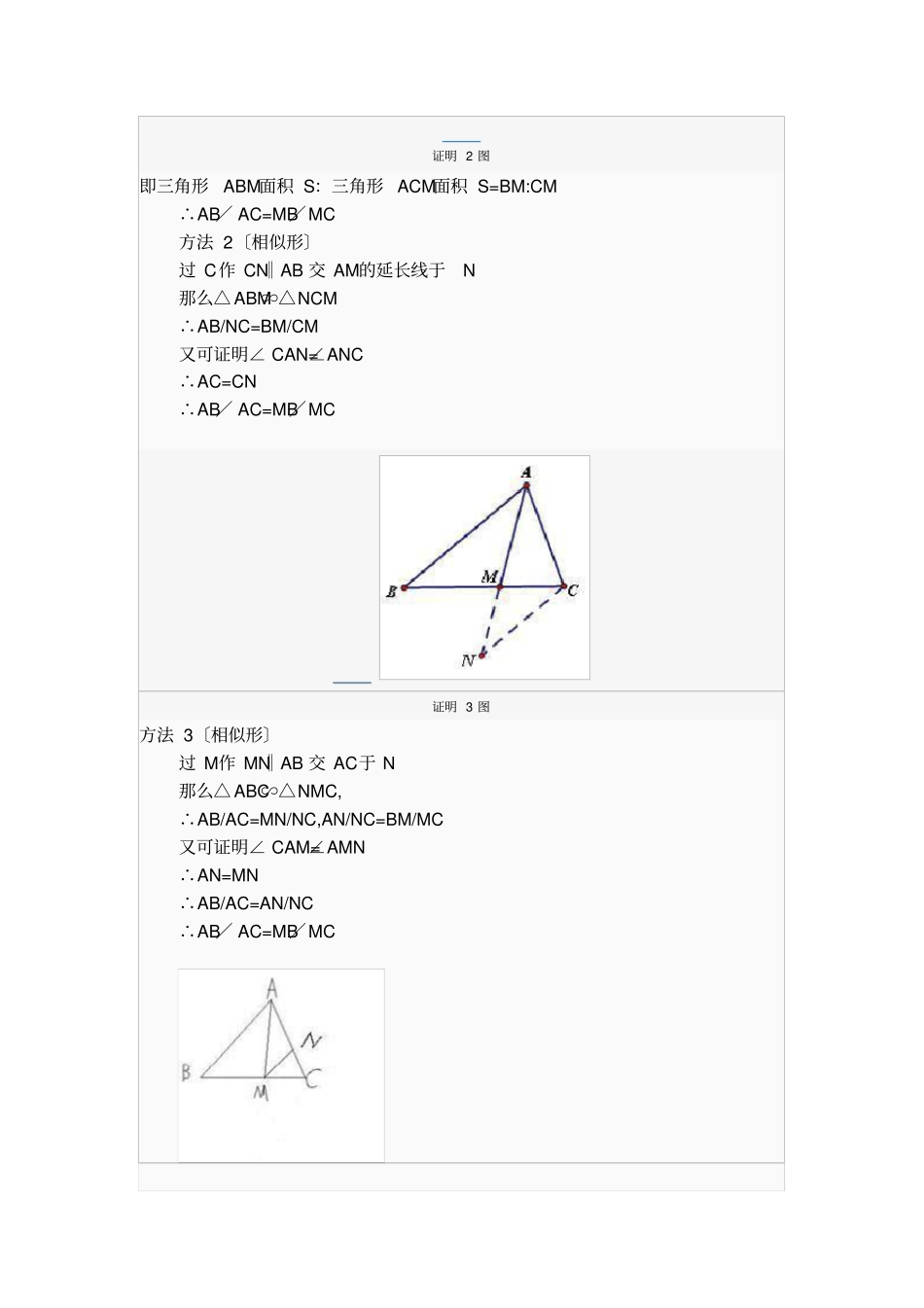
角平分线定理角平分线的定义:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线。■三角形的角平分线定义:三角形顶点到其内角的角平分线交对边的点连的一条线段,叫三角形的角平分线。【注】三角形的角平分线不是角的平分线,是线段。角的平分线是射线。■拓展:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等!(即内心)。■定理1:在角平分线上的任意一点到这个角的两边距离相等。■逆定理:在一个角的内部〔包括顶点〕,且到这个角的两边距离相等的点在这个角的角平分线上。■定理2:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例,如:在△ABC中,BD平分∠ABC,那么AD:DC=AB:BC提供四种证明方法:,如图,AM为△ABC的角平分线,求证AB/AC=MB/MC和证明1图证明:方法1:〔面积法〕S△ABM=(1/2)·AB·AM·sin∠BAM,S△ACM=(1/2)·AC·AM·sin∠CAM,∴S△ABM:S△ACM=AB:AC又△ABM和△ACM是等高三角形,面积的比等于底的比,证明2图即三角形ABM面积S:三角形ACM面积S=BM:CM∴AB/AC=MB/MC方法2〔相似形〕过C作CN‖AB交AM的延长线于N那么△ABM∽△NCM∴AB/NC=BM/CM又可证明∠CAN=∠ANC∴AC=CN∴AB/AC=MB/MC证明3图方法3〔相似形〕过M作MN‖AB交AC于N那么△ABC∽△NMC,∴AB/AC=MN/NC,AN/NC=BM/MC又可证明∠CAM=∠AMN∴AN=MN∴AB/AC=AN/NC∴AB/AC=MB/MC方法4〔正弦定理〕作三角形的外接圆,AM交圆于D,由正弦定理,得,证明4图AB/sin∠BMA=BM/sin∠BAM,∴AC/sin∠CMA=CM/sin∠CAM又∠BAM=∠CAM,∠BMA+∠AMC=180°sin∠BAM=sin∠CAM,sin∠BMA=sin∠AMC,∴AB/AC=MB/MC