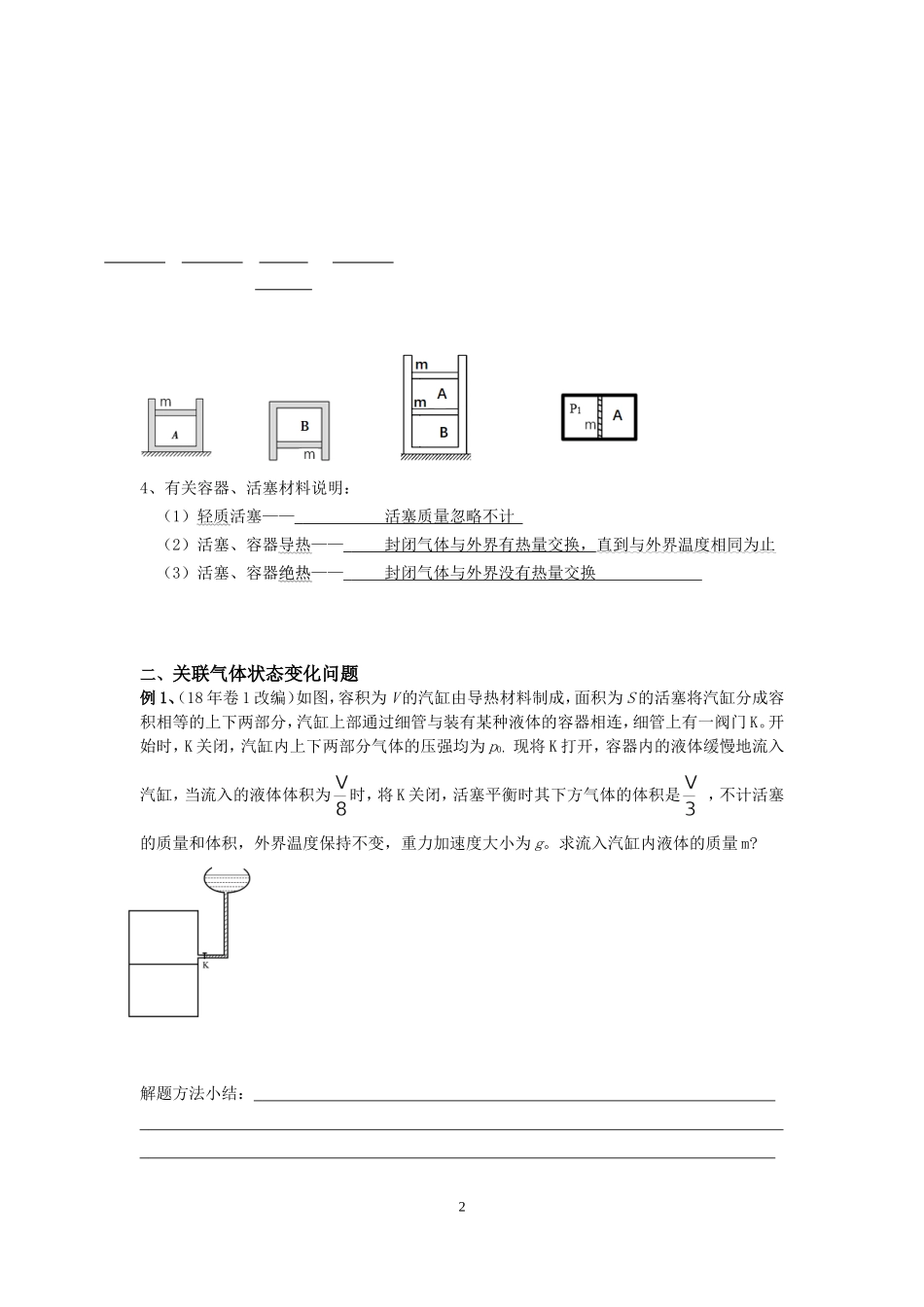
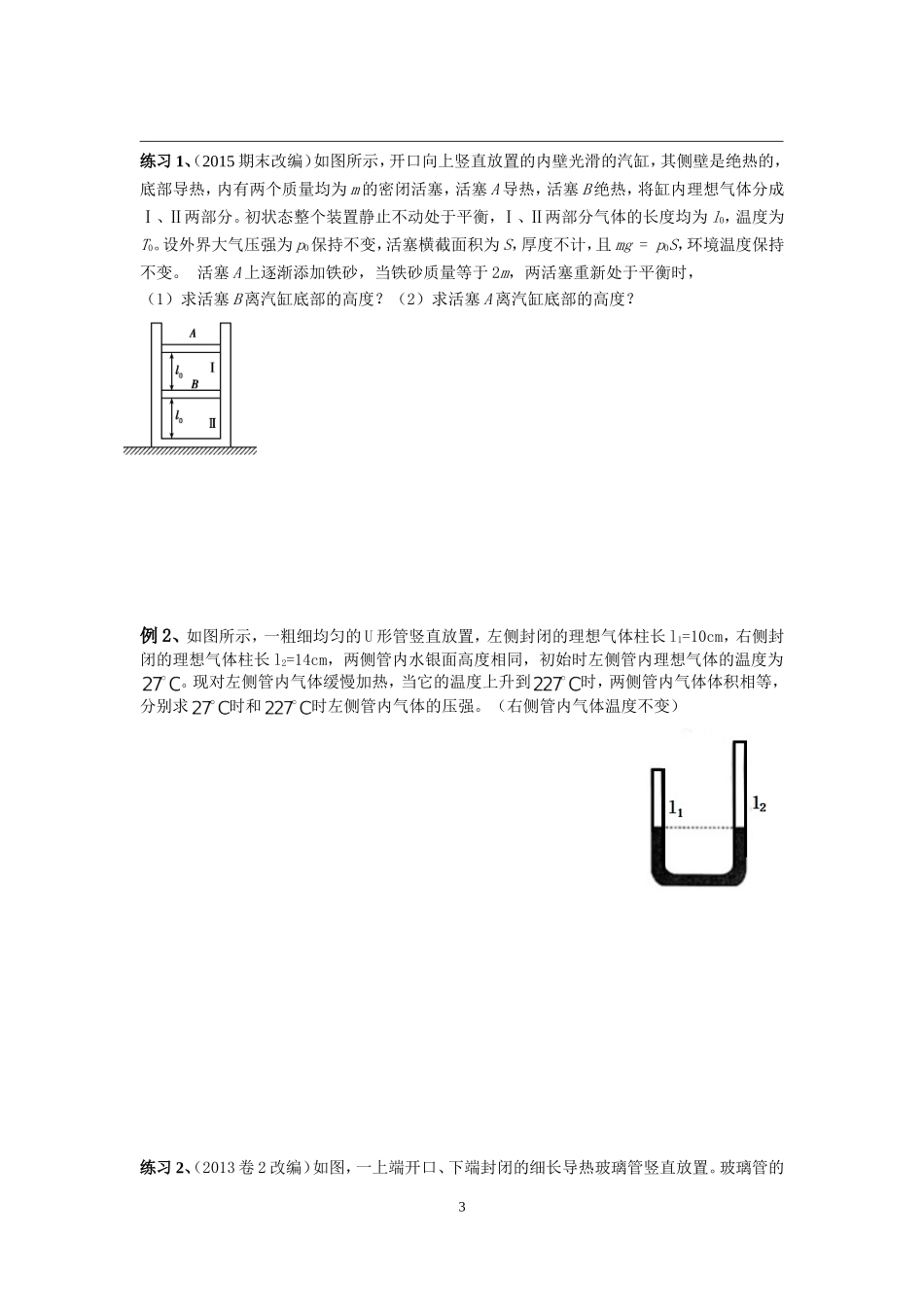
理想气体实验定律应用专题—关联气体状态变化问题姓名:班级:一、知识回顾:1、气体实验定律(1)玻意耳定律:(2)查理定律:(3)盖吕萨克定律:(4)理想气体状态方程:2、已知大气压强为p0=h0cmHg,P1=h1cmHg在图中各装置中水银柱均处于静止状态,求被封闭气体A、B的压强(用给定的字母表示)3、如图气缸内部横截面积均为S,活塞的质量均为m,已知大气压强为p0。重力加速度为g。求封闭气体A、B的压强各多大?(用给定的字母表示)14、有关容器、活塞材料说明:(1)轻质活塞——活塞质量忽略不计(2)活塞、容器导热——封闭气体与外界有热量交换,直到与外界温度相同为止(3)活塞、容器绝热绝热——封闭气体与外界没有热量交换二、关联气体状态变化问题例1、(18年卷1改编)如图,容积为V的汽缸由导热材料制成,面积为S的活塞将汽缸分成容积相等的上下两部分,汽缸上部通过细管与装有某种液体的容器相连,细管上有一阀门K。开始时,K关闭,汽缸内上下两部分气体的压强均为p0,现将K打开,容器内的液体缓慢地流入汽缸,当流入的液体体积为时,将K关闭,活塞平衡时其下方气体的体积是,不计活塞的质量和体积,外界温度保持不变,重力加速度大小为g。求流入汽缸内液体的质量m?解题方法小结:2练习1、(2015期末改编)如图所示,开口向上竖直放置的内壁光滑的汽缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成Ⅰ、Ⅱ两部分。初状态整个装置静止不动处于平衡,Ⅰ、Ⅱ两部分气体的长度均为l0,温度为T0。设外界大气压强为p0保持不变,活塞横截面积为S,厚度不计,且mg=p0S,环境温度保持不变。活塞A上逐渐添加铁砂,当铁砂质量等于2m,两活塞重新处于平衡时,(1)求活塞B离汽缸底部的高度?(2)求活塞A离汽缸底部的高度?例2、如图所示,一粗细均匀的U形管竖直放置,左侧封闭的理想气体柱长l1=10cm,右侧封闭的理想气体柱长l2=14cm,两侧管内水银面高度相同,初始时左侧管内理想气体的温度为。现对左侧管内气体缓慢加热,当它的温度上升到时,两侧管内气体体积相等,分别求时和时左侧管内气体的压强。(右侧管内气体温度不变)练习2、(2013卷2改编)如图,一上端开口、下端封闭的细长导热玻璃管竖直放置。玻璃管的3下部封有长lB=25.0cm的空气柱,中间有一段长h=25.0cm的水银柱,上部空气柱的长度lA=40.0cm。已知大气压强为p0=75.0cmHg。现将一活塞从玻璃管开口处缓慢往下推,使管下部空气柱长度变为lB′=20.0cm。假设活塞下推过程中没有漏气,求活塞最终到玻璃管底部的高度是多少?活塞下推的距离是多少?三、课后练习:1、如图,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞(两活塞面积相等)与两汽缸间均无摩擦。两汽缸内装有处于平衡状态的理想气体,开始时体积均为V0、温度均为T0。缓慢加热A中气体,停止加热达到稳定后,A中气体压强变为原来的1.2倍。设环境温度始终保持不变。则此时汽缸A中气体的体积VA=,温度TA=。2、在两端封闭、粗细均匀的U形细玻璃管内有一股水银柱,水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时,左、右两边空气柱的长度分别为l1=18.0cm和l2=12.0cm,左边气体的压强为12.0cmHg。现将U形管缓慢平放在水平桌面上,没有气体从管的一边通过水银逸入另一边。求U形管平放时两边空气柱的长度。在整个过程中,气体温度不变。43、如图所示,高为h、上端开口的气缸内壁光滑,除底部导热外,其余部分均绝热。在气缸顶部有一个厚度不计的绝热卡环,在气缸内有两个厚度不计的绝热轻质活塞A、B,它们距气缸底部的距离分别为和.活塞A、B之间封闭了一定质量的理想气体I,活塞B的下方封闭了一定质量的理想气体Ⅱ,气体I、Ⅱ的温度均为27°C.现利用电热丝对气体I缓慢加热,求:①活塞A刚好上升到卡环处时气体I的温度?此时气体Ⅱ各状态参数如何变化?②气体I的温度为800K时,活塞A、B间的距离。理想气体实验定律应用专题—关联气体状态变化问题参考答案例1、设活塞再次平衡后,活塞上方气体的体积为V1,压强为p1;下方气体的体积为V2,压强为p2,在活塞下移的过程中,活塞上下方...