直线与椭圆的位置关系VIP免费

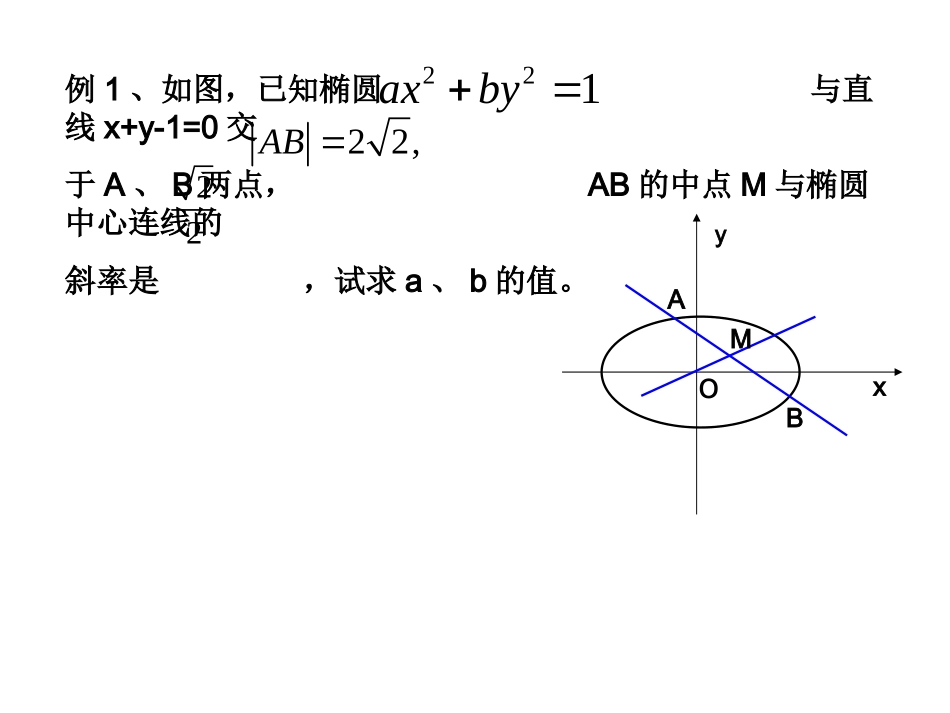
直线与椭圆的位置关系直线与椭圆的位置关系椭圆的简单几何性质(四)复习回顾：1、弦长公式：若直线AB与椭圆相交于两点，则212122111ABkxxyyk1122(,)(,)AxyBxy、例1、如图，已知椭圆与直线x+y-1=0交于A、B两点，AB的中点M与椭圆中心连线的斜率是，试求a、b的值。221axby22,AB22oxyABM..)0()0(1)(020121222200exaMFexaMFacecFcFbyaxyxM，求证：为离心率分别是椭圆两焦点，，、，上一点，是椭圆，设例2．Mll1xyF2F1O，对应的准线为，证明：与caxcF21)0(注：是椭圆上的点到焦点的距离，常把它们叫做焦半径。0201exaMFexaMF，0020222)(exaexcaexcaeedMF，对应的准线为，又与caxcF22)0(，aexcaeexcaxeedMF0202011)(引申:当点P与两焦点连线成钝角时,求P点的横坐标的取值范围.例3：求椭圆上一点P,使得点P与椭圆两焦点连线互相垂直.14922yx思考:椭圆xy22941的焦点为FF12、，点P为其上的动点，当FPF12为钝角时，则点P的横坐标的取值范围是____________.设P(x,y)，则||1533，PFaexx||2533PFaexx由余弦定理,有cos12FPF||||||||||()2222121221251952299xPFPFFFPFPFx12FPF为钝角21225191cos01052(9)9，即xFPFx353555x解之得.法二法二:(数形结合)以FF12为直径的圆交椭圆于PP12，1212，而、PPPxxxPP的坐标可由22225194xyxy12353555解得，PPxx例4、已知椭圆5x2+9y2=45，椭圆的右焦点为F，(1)求过点F且斜率为1的直线被椭圆截得的弦长.(2)判断点A(1,1)与椭圆的位置关系,并求以A为中点椭圆的弦所在的直线方程.例4:已知椭圆22195xy的焦点为12,FF,在直线:60lxy上找一点M,求以12,FF为焦点,通过点M且长轴最短的椭圆方程.2212016xy分析:∵椭圆的焦点为(2,0),(2,0)关键是怎样求出椭圆的长轴大小.思维挑战题:试确定实数m的取值范围,使得椭圆22143xy上存在关于直线2yxm对称的点.1122m【练习】112222byaxP是椭圆．设(a＞b＞0)上一点，是两个焦点，半焦距21FF、为c，则的最大值与最小值之差一定是（）.21PFPFA.1B.C.D.2a2b2cxOyPFQDBA122222byaxO的椭圆．如图，中心为(a＞b＞0)，F为焦点，A为顶点，准线l交x轴于B，P，Q在椭圆上，且PD⊥l于D，QF⊥AO，则椭圆其中正确的个数是；；；；的离心率是.AOFO⑸ABAF⑷BOAO⑶BFQF⑵PDPF⑴（）A.1个B.3个C.4个D.5个DD练习巩固:1.过椭圆221164xy内一点(2,1)M引一条弦,使弦被点M平分,求这条弦所在的直线方程.2.椭圆221164xy上的点到直线220xy最大距离是________.3.已知椭圆的焦点12(3,0),(3,0)FF且和直线90xy有公共点,则其中长轴最短的椭圆方程为______.240xy102214536xy２、弦长公式：设直线l与椭圆C相交于A(x1，y1)，B(x2，y2)，则|AB|＝,其中k是直线的斜率2121||kxx１、判断直线与椭圆位置关系的方法：解方程组消去其中一元得一元二次型方程△<0相离△=0相切△>0相交３、处理弦中点问题：“点差法”、“韦达定理”小结