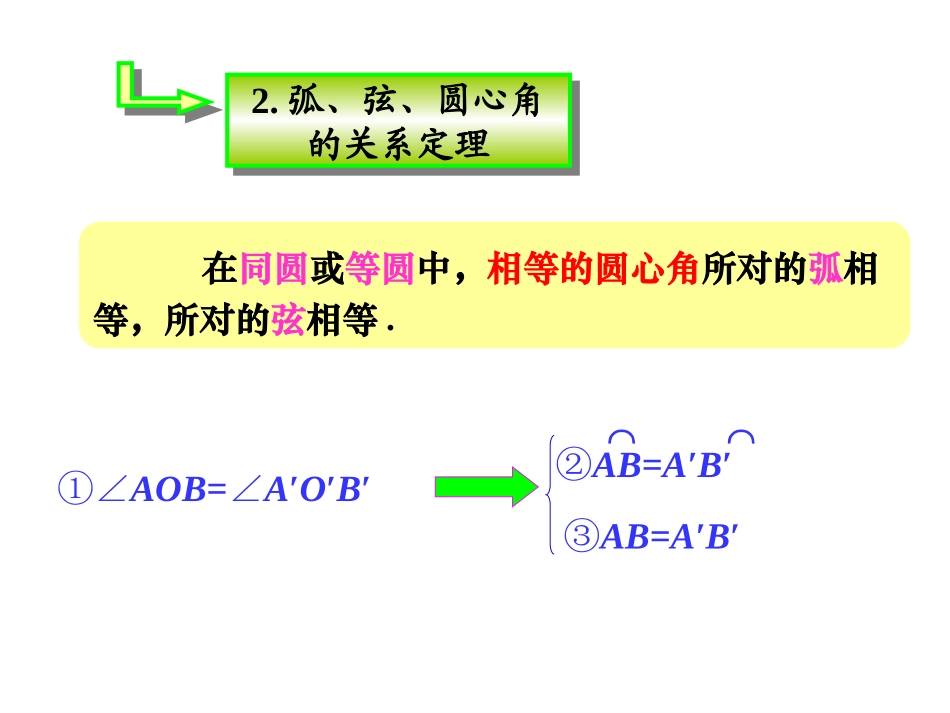
回顾旧知回顾旧知回顾旧知回顾旧知1.圆心角顶点在圆心,另两边与圆相交的角叫做圆心角.OAB在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.①∠AOB=∠A′O′B′②AB=A′B′⌒⌒③AB=A′B′2.弧、弦、圆心角的关系定理2.弧、弦、圆心角的关系定理学习目标:•1.记住圆周角的概念,记住圆周角的两个特征•2.熟记定理的内容并会简单的应用;•学习重点:圆周角的概念和圆周角定理•学习难点:圆周角定理的证明中由“一般到特殊”的数学思想方法和完全归纳的数学思想•问题:如图所示的⊙O,观察像∠EAF、∠EBF、∠ECF这样的角,•它们有什么特点?ABOFEC•1、圆周角定义:________________________叫圆周角.•特征:1.角的顶点在_______;•2.角的两边都_______________________.•练习:•1、下列各图中,哪一个角是圆周角?()•ABCD•练习2.图3中有几个圆周角?()A.2个B.3个C.4个D.5个.•练习3.写出图4中的圆周角:_______________________________•练习4.在同圆中,一条弧所对的圆心角有几个?圆周角有几个?画图表示.ABDCABC图3图4•2、度量猜想关系:•1.一条弧上所对的圆周角的个数有多少个?__________________•2.同弧所对的圆周角的度数是否发生变化?__________________•3.同弧上的圆周角与圆心角有什么关系?____________________________________•试证明你的结论:•(1)如图1设圆周角∠ABC的一边BC是⊙O的直径•(2)如图2圆周角∠ABC的两边AB、AC在一条直径BD的两侧•(3)圆周角∠ABC的两边AB、AC在一条直径BD的同侧DAOCBBCOAAODCB图1图2图3•总结:•圆周角定理:在同圆或等圆中,同弧或等弧所对的_________相等,都等于_____________________的一半.•3、自主探究:•问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?•问题2、如图2,AB是⊙O的直径,C是⊙O上任意点,你能确定∠ACB的度数吗?•问题3、如图3,圆周角∠BCA=90°,弦AB经过圆心O吗?AOCBBCOAAOEDCB图3图2图1•圆周角定理的推论1:半圆(或直径)所对的圆周角是___________;_______________所对的弦是直径.•在同圆或等圆中,如果两个圆周角相等,它们所对的________________________一定相等.•三、课堂小结:这节课我们学习了一个新的概念和两个重要的定理,都能记住了吗?•四、课堂作业:•1.顶点在__________上,并且两边都与圆__________的角叫圆周角.•2.在同圆或等圆中,_______或_______所对的圆周角相等,都等于这条弧所对的_______的一半.•3.在同圆或等圆中,相等的圆周角所对的弧也________________________.•4.半圆(或直径)所对的圆周角是__________,90°的圆周角所对的弦是______________.•5.如图(1)所示,点A、B、C在⊙O上,连接OA、OB,若∠ABO=25°,则∠C=_____.•6.如图(2)所示,AB是⊙O的直径,AC是弦,若∠ACO=32°,则∠COB=_______.•7.如图(3)所示,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,若OD=5cm,•则BE=______.•8.如图(4)所示,点A、B、C在⊙O上,已知∠B=60°,则∠CAO=____________.••(1)(2)(3)(4)BCOABAOCEBCOAAODCB