汽车行驶的路程VIP免费

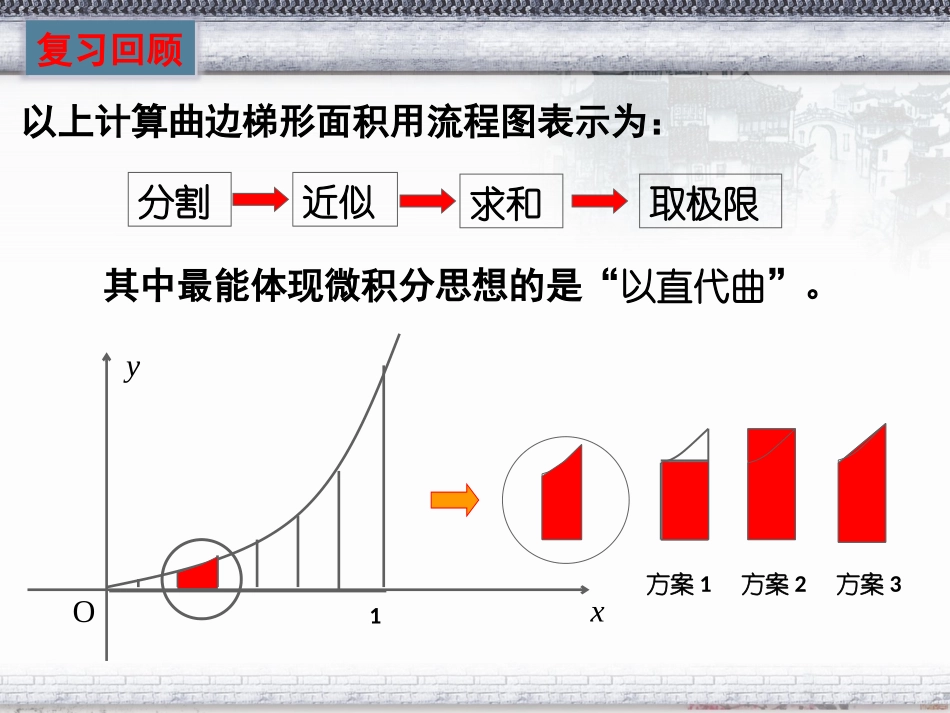
汽车行驶的路程分割近似求和取极限以上计算曲边梯形面积用流程图表示为：其中最能体现微积分思想的是“以直代曲”。复习回顾复习回顾xyO1方案1方案2方案3f(x2)f(xi)xiy=f(x)baxyOx1xi-1xixn-1x2xif(xi)x1x2f(x1)•在[a,b]中任意插入n-1个分点．•得n个小区间：[xi1,xi](i=1,2,···,n)．•把曲边梯形分成n个细窄曲边梯形．•任取xi[xi1,xi],以f(xi)Dxi近似代替第i个窄曲边梯形的面积．•区间[xi1,xi]的长度Dxixixi1．•曲边梯形的面积近似为：Aniiixf1)(．问题1：汽车以速度v作匀速直线运动时，经过时间t所行驶的路程为S＝vtSvtO问题2：如果汽车作变速直线运动，在t时刻的速度为：(单位：km/h），那么它在0≤t≤1(单位：h)这段时间内行驶的路程（单位：km）是多少？22vttVtOA1A2A3An分析：在每个小区间上，由于()vt的变化很小，可以近似的看作汽车作于速直线运动，从而求得汽车在每个小区间上行驶路程的近似值，在求和得S（单位：km）的近似值，最后让n趋紧于无穷大就得到S（单位：km）的精确值．思想方法：分割近似代替求和逼近解：（1）分割在时间区间[0,1]上等间隔地插入n-1个分点，将区间等分成n个小区间：],nn,n1n[,],ni,n1i[,],n2,n1[],n1,0[n1n1init每个区间的长度为：上行驶的路程分别记作把汽车在时间段],nn,n1n[,],ni,n1i[,],n2,n1[],n1,0[.S,,S,,S,Sni21显然，1niiSS（2）近似代替当n很大，即t很小时，在区间1,iinn上，可以认为它近似地以时刻1in处的速度2112iivnn作匀速直线运动。21112iiiiSSvtnnn2112(1,2,,)iinnnn①（3）求和由①得，21111112nnnniiiiiiSSvtnnnn=221111102nnnnnn=222311212nn=3121126nnnn=11111232nn从而得到S的近似值11111232nSSnn（4）取极限当n趋向于无穷大时，即t趋向于0时，11111232nSnn趋向于S，从而有111limlimnnnniiSSvnn1115lim112323nnn。思考：结合求曲边梯形面积的过程，你认为汽车行驶的路程S与由直线0,1,0ttv和曲线22vt所围成的曲边梯形的面积有什么关系？结合上述求解过程可知，汽车行驶的路程limnnSS在数据上等于由直线0,1,0ttv和曲线22vt所围成的曲边梯形的面积．思考如果物体做变速直线运动，速度函数v(t)，那么我们可以采用分割、近似代替、求和、取极限的方法求出它在任意时段所作的位移S。