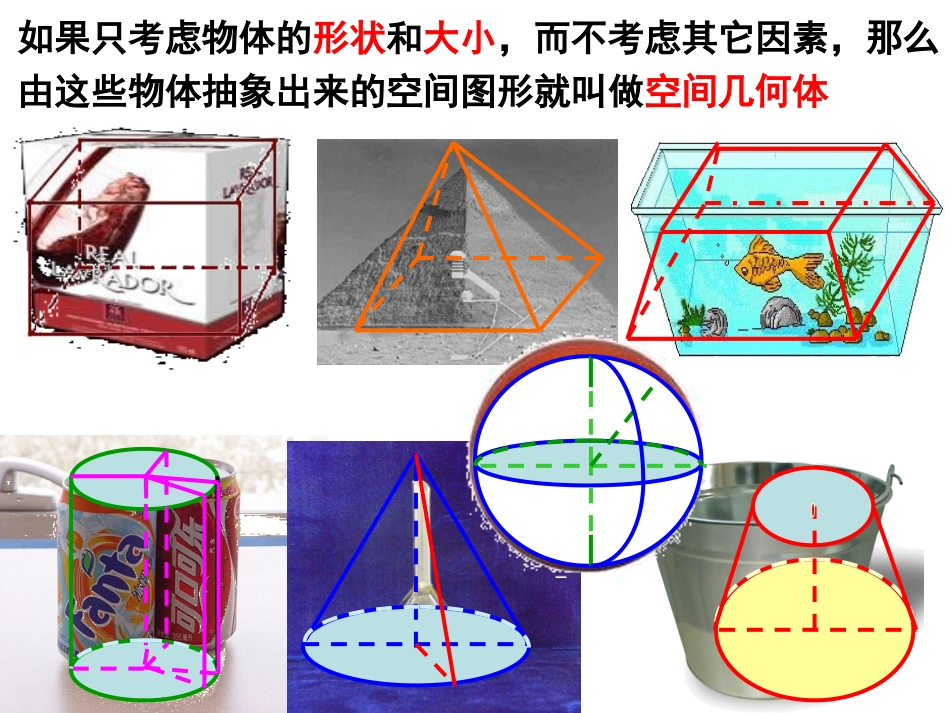
空间几何体第一课时问题1:观察下面的实物图片,这些图片中的物体具有怎样的形状?属于哪种空间几何体?如果只考虑物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体多面体由若干个平面多边形围成的几何体.顶点面棱BADCB1A1D1C1旋转体由一个平面图形绕它所在平面内的一条直线旋转所形成的封闭几何体.轴生活中的立体图形1235467简单空间几何体的分类多面体旋转体简单空间几何体柱体锥体台体球体圆柱棱柱圆锥棱锥圆台棱台1、棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱相邻侧面的公共边叫做棱柱的侧棱侧面与底的公共顶点叫做棱柱的顶点两个互相平行的平面叫做棱柱的底面其余各面叫做棱柱的侧面底面侧面侧棱顶点棱柱的结构特征.exe三棱柱四棱柱五棱柱侧棱不垂直于底的棱柱叫做斜棱柱。侧棱垂直于底的棱柱叫做直棱柱。底面是正多边形的直棱柱叫做正棱柱。2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……3、棱柱的表示法:用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE-A1B1C1D1E1。ABCDA1A1B1B1C1C1D1ABCA1B1C1D1E1ABCED问题1:由棱柱的结构特征可知:棱柱有两个面互相平行,其余各面都是平行四边形,反过来,成立吗?提示:不一定成立.如图所示几何体有两个面平行,其余各面都是平行四边形,但不满足“每相邻两个侧面的公共边互相平行”,故它不是棱柱.1、棱锥的定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥这个多边形面叫做棱锥的底面有公共顶点的各个三角形叫做棱锥的侧面各侧面的公共顶点叫做棱锥的顶点相邻侧面的公共边叫做棱锥的侧棱SABCDE底面顶点侧面侧棱棱锥的结构特征.exe2、棱锥的分类:按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……ABCDS3、棱锥的表示法:用表示顶点和底面的字母表示,如:四棱锥S-ABCD。4、如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。1、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。侧面侧棱上底面下底面棱台的结构特征.exe2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:棱台用表示上、下底面各顶点的字母来表示,如:棱台ABCDE-A1B1C1D1E1。4、用正棱锥截得的棱台叫做正棱台。E'DEABCD'A'B'C'棱柱、棱锥、棱台的结构特征比较结构特征棱柱棱锥棱台定义底面侧面侧棱平行于底面的截面过不相邻两侧棱的截面两底面是全等的多边形平行四边形平行且相等与两底面是全等的多边形平行四边形多边形三角形相交于顶点与底面是相似的多边形三角形两底面是相似的多边形梯形延长线交于一点与两底面是相似的多边形梯形下列命题是否正确?有一个面是多边形,其余各面都是三角形的立体图形一定是棱锥.辨析明矾晶体四、圆柱的结构特征:矩形O1OA’B’AOBO’1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱(4)无论旋转到什么位置,不垂直于轴的边都叫做圆柱的母线(3)平行于轴的边旋转而成的曲面叫做圆柱的侧面(2)垂直于轴的边旋转而成的圆面叫做圆柱的底面(1)旋转轴叫做圆柱的轴圆柱的结构特征.exe轴母线底面侧面2、圆柱的表示法:用表示它的轴的字母表示,如圆柱OO1。OO1AA’B’B五、圆锥的结构特征:直角三角形SAOSABO(4)无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线(3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面(2)垂直于轴的边旋转而成的圆面叫做圆锥的底面(1)旋转轴叫做圆锥的轴1、定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转而成的面所围成的旋转体叫做圆锥圆锥的结构特征.exeOSBA轴底面侧面母线2、圆锥的表示法:用表示它的轴的字母表示,如圆锥SO。六、圆台的结构特征:定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台OO'侧面母线上底面下底面OO'...