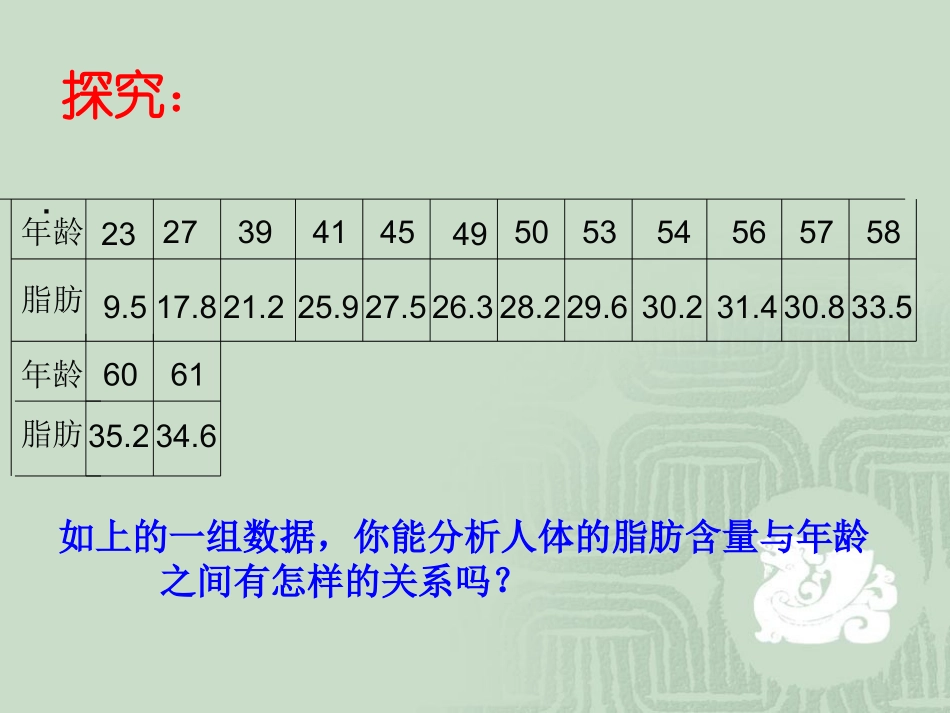
两个变量的线性关系.遂宁中学罗辉新教材课件引入:当一个变量y随另一个变量x变化时,存在许多关系.这里,讨论两类关系:1.确定关系如函数关系、公式等.2.不确定关系中的相关关系商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系.在统计中,由于变量之间关系的广泛性和不确定性,所以存在大量的相关关系.我们最关心的是变量之间的相关关系是否具有直线关系--------线性相关,如何确定直线关系-------线性回归方程.探究:.年龄脂肪239.52717.83921.24125.9454927.526.35028.25329.65430.25631.45730.8年龄脂肪5833.56035.26134.6如上的一组数据,你能分析人体的脂肪含量与年龄之间有怎样的关系吗?从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加”这一规律.而表中各年龄对应的脂肪数是这个年龄人群的样本平均数.我们也可以对它们作统计图、表,对这两个变量有一个直观上的印象和判断.下面我们以年龄为横轴,脂肪含量为纵轴建立直角坐标系,作出各个点,称该图为散点图。如图:O20253035404550556065年龄脂肪含量510152025303540从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。但有的两个变量的相关,如下图所示:如高原含氧量与海拔高度的相关关系,海平面以上,海拔高度越高,含氧量越少。作出散点图发现,它们散布在从左上角到右下角的区域内。又如汽车的载重和汽车每消耗1升汽油所行使的平均路程,称它们成负相关.O我们再观察它的图像发现这些点大致分布在一条直线附近,像这样,如果在散点图中,点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线,该直线叫回归方程。那么,我们该怎样来求出这个回归方程?20253035404550556065年龄脂肪含量0510152025303540..方案1、先画出一条直线,测量出各点与它的距离,再移动直线,到达一个使距离的和最小时,测出它的斜率和截距,得回归方程。20253035404550556065年龄脂肪含量0510152025303540如图:.方案2、在图中选两点作直线,使直线两侧的点的个数基本相同。20253035404550556065年龄脂肪含量0510152025303540方案3、如果多取几对点,确定多条直线,再求出这些直线的斜率和截距的平均值作为回归直线的斜率和截距。而得回归方程。如图我们还可以找到更多的方法,但这些方法都可行吗?科学吗?准确吗?怎样的方法是最好的?20253035404550556065年龄脂肪含量0510152025303540我们把由一个变量的变化去推测另一个变量的方法称为回归方法。).,(),,(),(221,1nnyxyxyx设两个具有线性相关关系的变量的一组数据为则其线性回归方程为axbyniiniiiniiniiixnxyxnyxxbyaxxyyxxb1221121)()())((回归方程),(yxaxby必过样本中心点以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。1.ABCD在下列量与量的关系中,是相关关系的是①正方体的体积与棱长间的关系;②一块农田的水稻产量与施肥量的关系;③人的身高与年龄;④家庭的支出与收入;⑤某户家庭用电量与电价间的关系..②③.③④.④⑤.②③④DD.①是函数关系,⑤无关系,解析:故选练习2.ABCDxyxyxy在画两个变量的散点图时,下面哪个叙述是正确的.预报变量在轴上,解释变量在轴上.解释变量在轴上,预报变量在轴上.可以选择两个变量中任意一个变量在轴上.可以选择两个变量中任意一个变量在轴上B3.()A1CD:B下列说法中正确的是.任何两个变量之间都有相关关系.球的体积与该球的半径具有相关关系.农作物的产量与施化肥量之间是一种确定性的关系.某商品的生产量与该商品的销售价格之间是一种非例确定性的关系DABC""D概念错误,是函数关系,中确定性说法错解:误.析答案:397.1973.93.10A145.83cmB145.83cmC145.83cmD145.83cmyx一位母亲记录了儿子~岁的身高,由此建立的身高与年龄的回归模型为用这个模型预测这个...