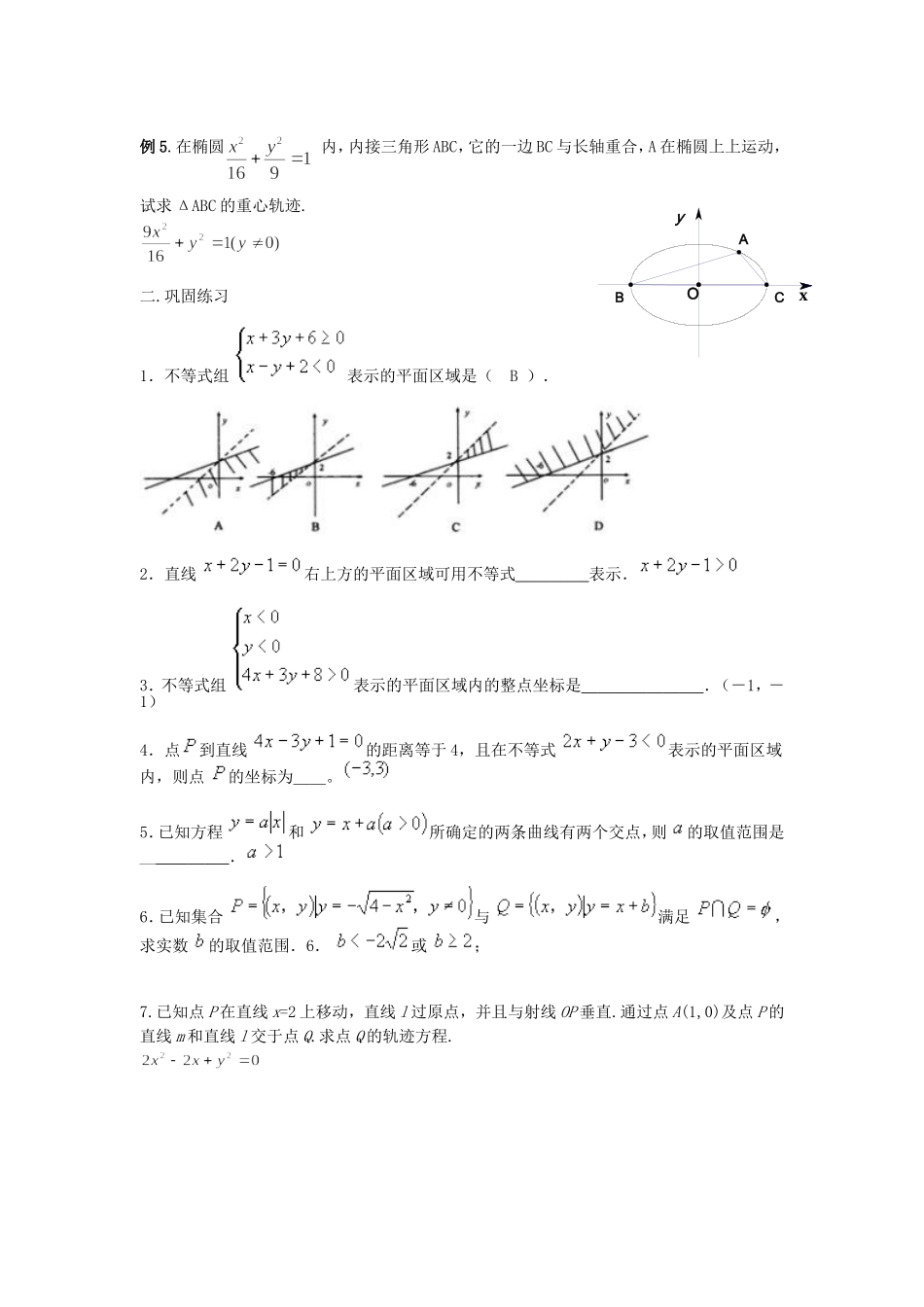
高二数学期末复习之线性规划与曲线方程http://www.dearedu.com一.典型例题例1解线性规划问题:求的最大值,使式中的x、y满足约束条件.解:作出可行域,见图,五边形OABCD表示的平面区域.作出直线将它平移至点B,显然,点B的坐标是可行域中的最优解,它使达到最大值,解方程组得点B的坐标为(9,2).∴例2在正三角形内有一动点,已知到三个顶点的距离分别为、、,且有,求点轨迹方程.分析、略解:首先应建立坐标系,以正三角形一边所在的直线为一个坐标轴,这条边的垂直平分线为另一个轴,建立直角坐标系比较简单,如图3所示.设、的坐标为、,则的坐标为,的坐标为.根据条件,代入坐标可得化简得①由于题目中要求点在三角形内,所以,在结合①式可进一步求出、的范围,最后曲线方程可表示为例3:已知两定点、,一动点与、连线的夹角为,求动点的轨迹方程.解:设,由夹角公式有即化简得(1)当时,;(2)当时,.例4.已知的顶点固定,其对边为定长,当沿一定直线移动时,求的外心的轨迹方程.4.以l为轴,边上的高为轴,建立直角坐标系,设的坐标为,的轨迹方程为;例5.在椭圆内,内接三角形ABC,它的一边BC与长轴重合,A在椭圆上上运动,试求ΔABC的重心轨迹.二.巩固练习1.不等式组表示的平面区域是(B).2.直线右上方的平面区域可用不等式表示.3.不等式组表示的平面区域内的整点坐标是.(-1,-1)4.点到直线的距离等于4,且在不等式表示的平面区域内,则点的坐标为__。5.已知方程和所确定的两条曲线有两个交点,则的取值范围是__.6.已知集合与满足,求实数的取值范围.6.或;7.已知点P在直线x=2上移动,直线l过原点,并且与射线OP垂直.通过点A(1,0)及点P的直线m和直线l交于点Q.求点Q的轨迹方程.xyOABC