高中数学 第一章 立体几何初步 6 6.2 垂直关系的性质课时跟踪检测 北师大版必修2-北师大版高一必修2数学试题VIP免费

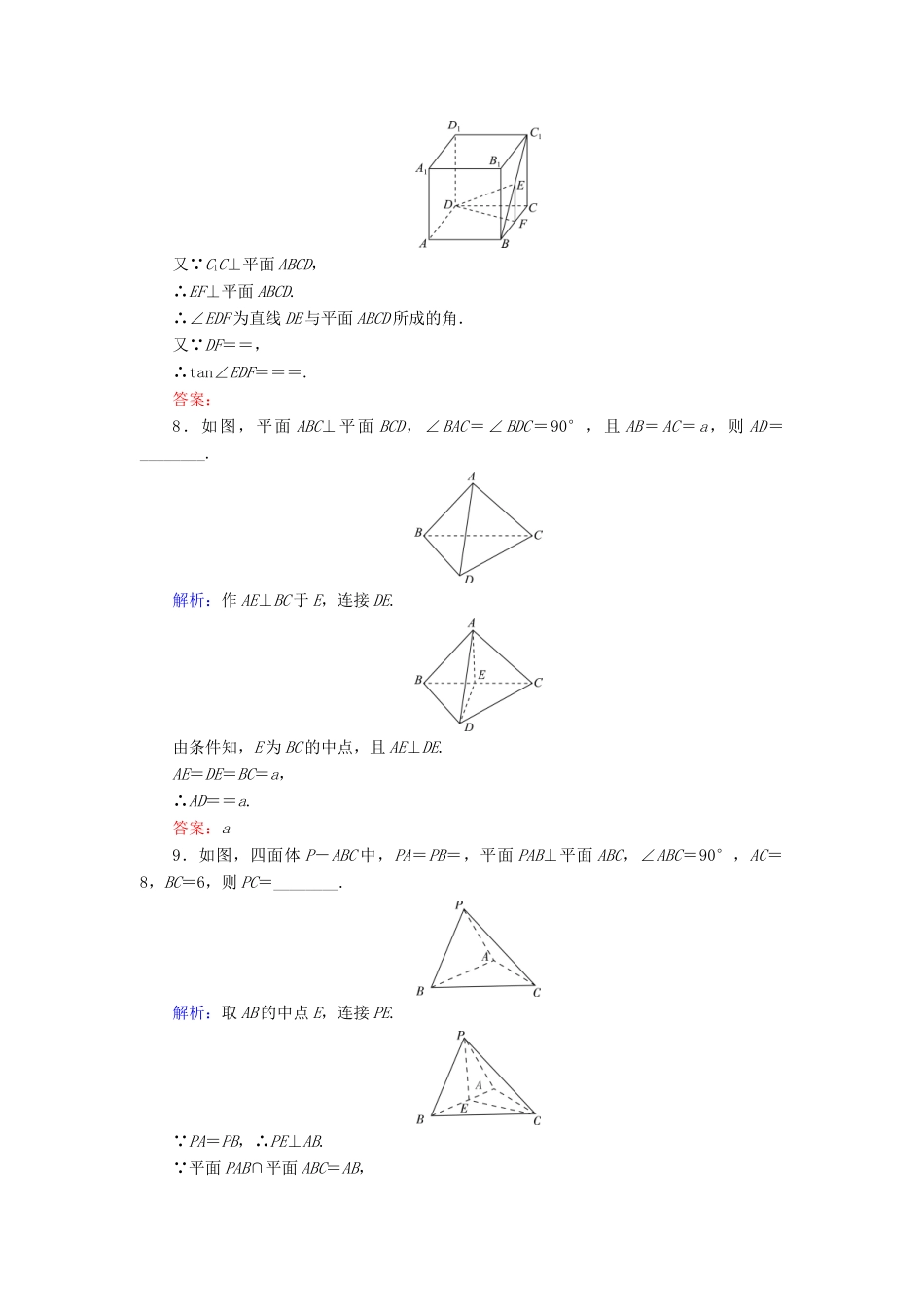
6.2垂直关系的性质课时跟踪检测一、选择题1．下面说法正确的是()A．若mα，lα，则m∥lB．若l⊥α，α∥β，则l⊥βC．若m∥n，nα，则m∥αD．若m⊥l，m⊥n，则l∥n解析：A中，mα，但m可能与α相交，此时m与l不平行，A错；C中，m也可以在α内，C错；D中，l与n还可能异面或相交，D错．答案：B2．若有平面α与β，且α∩β＝l，α⊥β，P∈α，P∉l，则下列命题中的假命题为()A．过点P且垂直于α的直线平行于βB．过点P且垂直于l的平面垂直于βC．过点P且垂直于β的直线在α内D．过点P且垂直于l的直线在α内解析：对于D，过点P垂直于l的直线可能在α内，也可能不在α内．答案：D3．下列命题正确的是()A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相离，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行解析：若两条直线和同一平面所成角相等，这两条直线可能平行，也可能为异面直线，也可能相交，故A错；当两个平面相交时，也满足条件，故B错；若两个平面垂直于同一个平面，两平面可以平行，也可以相交，故D错．答案：C4．如图，设平面α∩β＝EF，AB⊥α，CD⊥α，垂足分别是B、D，如果增加一个条件，就能推出BD⊥EF，这个条件不可能是下面四个选项中的()A．AC⊥βB．AC⊥EFC．AC与BD在β内的射影在同一条直线上D．AC与α、β所成的角相等解析： AB⊥α，CD⊥α，∴AB∥CD，∴A，B，C，D四点共面．选项A，B中的条件都能推出EF⊥平面ABDC，则EF⊥BD.选项C中，由于AC与BD在β内的射影在同一条直线上，所以平面ABDC与平面β垂直，又 EF⊥AB，∴EF⊥平面ABDC，∴EF⊥BD.选项D中，若AC∥EF，则AC与α，β所成角也相等，但不能推出BD⊥EF.答案：D5．如图，在正四棱锥S－ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论中恒成立的个数为()①EP⊥AC；②EP∥BD；③EP∥面SBD；④EP⊥面SAC.A．1个B．2个C．3个D．4个解析：如图，平面EMN∥平面SBD，EP平面EMN，∴EP∥平面SBD，又 AC⊥平面SBD，∴AC⊥平面EMN，又 EP平面EMN，∴AC⊥EP，即EP⊥AC，则①③正确，②④错误．答案：B6．如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则点C1在平面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部解析：如图，连接AC1， ∠BAC＝90°，∴AC⊥AB.又AC⊥BC1，AB∩BC1＝B，∴AC⊥平面ABC1.又ACABC，∴平面ABC1⊥平面ABC，且平面ABC1∩平面ABC＝AB，∴点C1在平面ABC上的射影必在直线AB上．答案：A二、填空题7．如图，在棱长为2的正方体ABCD－A1B1C1D1中，E是BC1的中点，则直线DE与平面ABCD所成角的正切值为________．解析：取BC的中点F，连接EF，DF.则EF∥C1C，且EF＝C1C＝1.又 C1C⊥平面ABCD，∴EF⊥平面ABCD.∴∠EDF为直线DE与平面ABCD所成的角．又 DF＝＝，∴tan∠EDF＝＝＝.答案：8．如图，平面ABC⊥平面BCD，∠BAC＝∠BDC＝90°，且AB＝AC＝a，则AD＝________.解析：作AE⊥BC于E，连接DE.由条件知，E为BC的中点，且AE⊥DE.AE＝DE＝BC＝a，∴AD＝＝a.答案：a9．如图，四面体P－ABC中，PA＝PB＝，平面PAB⊥平面ABC，∠ABC＝90°，AC＝8，BC＝6，则PC＝________.解析：取AB的中点E，连接PE. PA＝PB，∴PE⊥AB. 平面PAB∩平面ABC＝AB，又平面PAB⊥平面ABC，∴PE⊥平面ABC，连接CE，则PE⊥CE.∠ABC＝90°，AC＝8，BC＝6，∴AB＝2，PE＝＝，CE＝＝，PC＝＝7.答案：7三、解答题10．(2018·全国卷Ⅱ)如图，在三棱锥P－ABC中，AB＝BC＝2，PA＝PB＝PC＝AC＝4，O为AC的中点．(1)证明：PO⊥平面ABC；(2)若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．解：(1)证明：因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2.连接OB.因为AB2＋BC2＝AC2，所以△ABC为等腰直角三角形，且OB⊥AC，且OB＝AC＝2.由OP2＋OB2＝PB2知，OP⊥OB.由OP⊥OB，OP⊥AC且OB∩AC＝O知，PO⊥平面ABC.(2)作CH⊥OM，垂足为H.又由(1)可得OP⊥CH，所以CH⊥平面POM.故CH的长为点C到平面POM的距离．由题设可知...