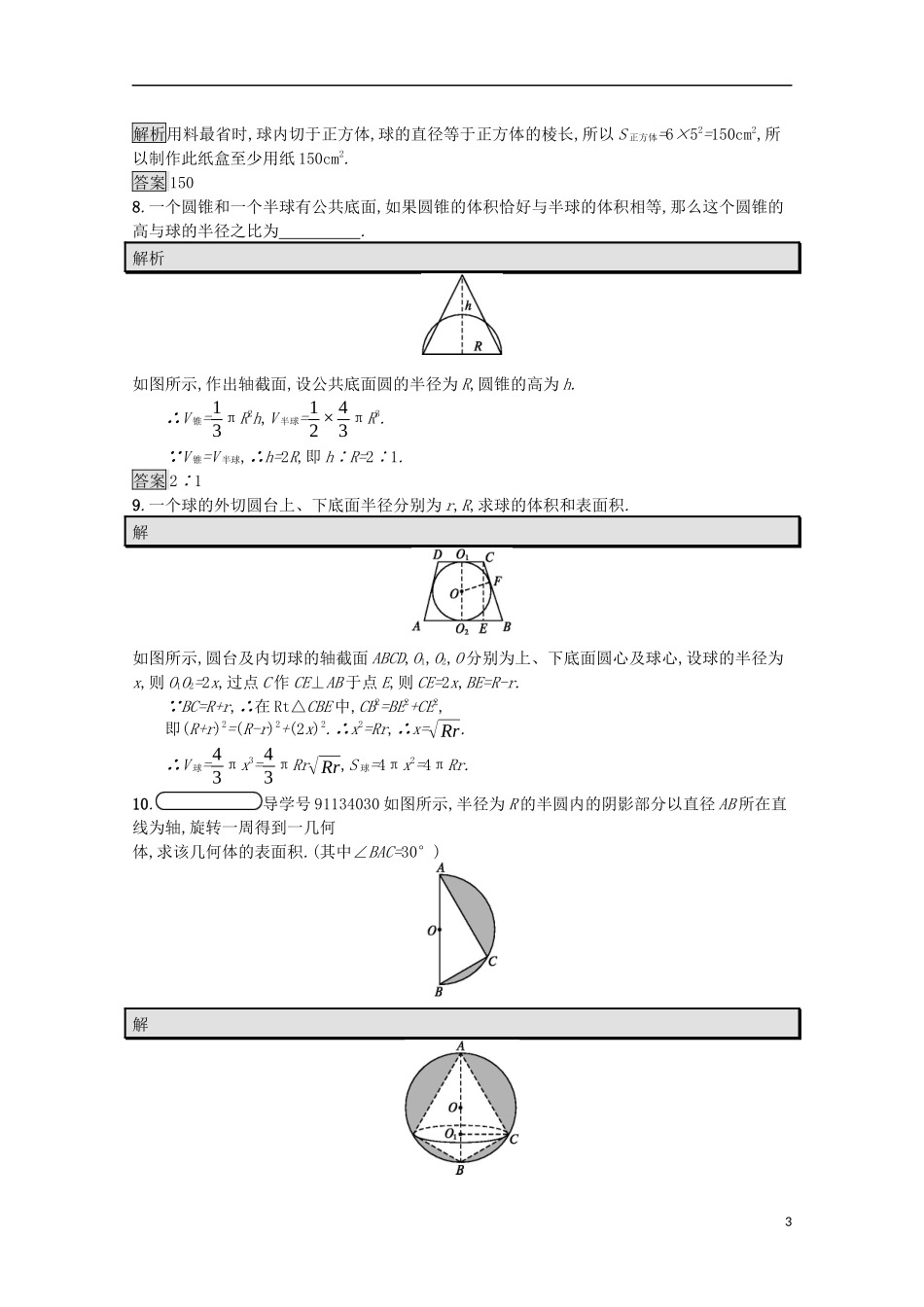
7.3球课后篇巩固探究1.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为()A.RB.2RC.3RD.4R解析设圆柱的高为h,则πR2h=3×43πR3,故h=4R.答案D2.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积之比为()A.1∶2∶3B.2∶3∶4C.3∶2∶4D.3∶1∶2解析V圆柱=2πR3,V圆锥=13πR2·(2R)=2π3R3,V球=43πR3.则体积之比为:2∶23∶43,即3∶1∶2.答案D3.有64个直径都为a4的球,记它们的体积之和为V甲,表面积之和为S甲,一个直径为a的球记其体积为V乙,表面积为S乙,则()A.V甲>V乙,S甲>S乙B.V甲S乙C.V甲=V乙,S甲>S乙D.V甲=V乙,S甲S乙.答案C4.如图所示,一个三棱锥的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积为()A.7π2cm2B.19πcm2C.14πcm2D.7πcm21解析该三棱锥可以看作是一个长、宽、高分别等于3cm,1cm,2cm的长方体的一部分,其外接球就是长方体的外接球.长方体的体对角线长为√12+22+32=√14(cm),此即为外接球的直径2R,于是外接球表面积S=4πR2=14πcm2.答案C5.如图所示,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,若不计容器的厚度,则球的体积为()A.500π3cm3B.866π3cm3C.1372π3cm3D.2048π3cm3解析设球半径为R,由题可知R,R-2,正方体棱长一半可构成直角三角形,即R2=(R-2)2+42,得R=5,所以球的体积为43π×53=5003π(cm3),故选A.答案A6.如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积S为()A.17π+3√17πB.20π+5√17πC.22πD.17π+5√17π解析由已知可得该几何体是一个圆台和一个半球形成的组合体,圆台的上底面半径r=2,下底面半径R=3,母线l=√42+12=√17,所以圆台的侧面积为π(R+r)l=5√17π,圆台的下底面面积为πR2=9π.又半球的半径为2,所以半球面的面积为2π·22=8π.所以几何体的表面积S=5√17π+9π+8π=17π+5√17π.故选D.答案D7.要把直径为5cm的钢球放入一个正方体有盖纸盒中,请问制作出此纸盒至少要用纸cm2.2解析用料最省时,球内切于正方体,球的直径等于正方体的棱长,所以S正方体=6×52=150cm2,所以制作此纸盒至少用纸150cm2.答案1508.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥的高与球的半径之比为.解析如图所示,作出轴截面,设公共底面圆的半径为R,圆锥的高为h.∴V锥=13πR2h,V半球=12×43πR3.∵V锥=V半球,∴h=2R,即h∶R=2∶1.答案2∶19.一个球的外切圆台上、下底面半径分别为r,R,求球的体积和表面积.解如图所示,圆台及内切球的轴截面ABCD,O1,O2,O分别为上、下底面圆心及球心,设球的半径为x,则O1O2=2x,过点C作CE⊥AB于点E,则CE=2x,BE=R-r.∵BC=R+r,∴在Rt△CBE中,CB2=BE2+CE2,即(R+r)2=(R-r)2+(2x)2.∴x2=Rr,∴x=√Rr.∴V球=43πx3=43πRr√Rr,S球=4πx2=4πRr.10.导学号91134030如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积.(其中∠BAC=30°)解3如图所示,过点C作CO1⊥AB于点O1.在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,∴AC=√3R,BC=R,CO1=√32R,∴S球=4πR2,S圆锥AO1侧=π×√32R×√3R=32πR2,S圆锥BO1侧=π×√32R×R=√32πR2,∴S几何体表=S球+S圆锥AO1侧+S圆锥BO1侧=112πR2+√32πR2=11+√32πR2.故旋转所得几何体的表面积为11+√32πR2.4