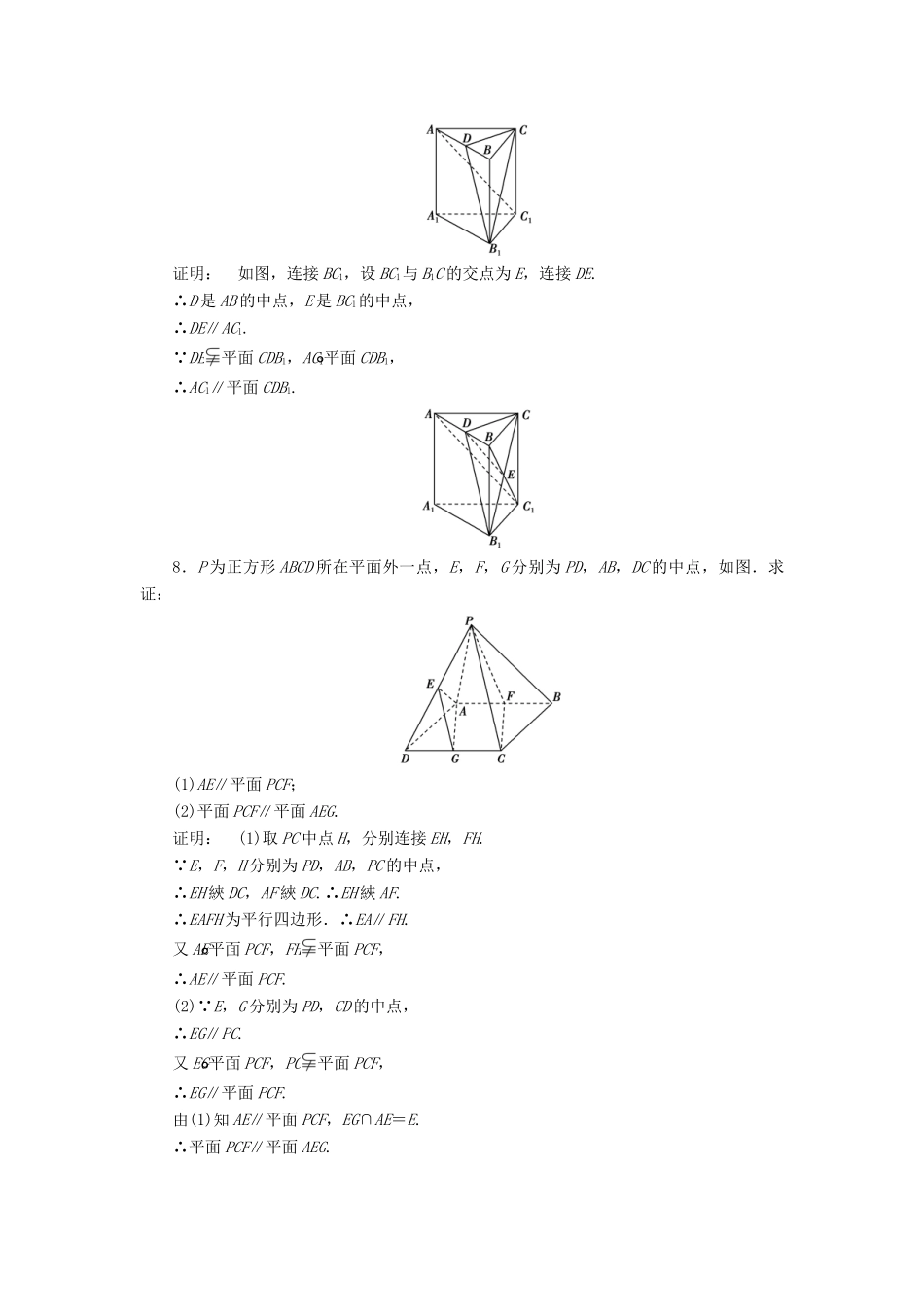
2016-2017学年高中数学第一章立体几何初步1.5.1平行关系的判定高效测评北师大版必修2一、选择题(每小题5分,共20分)1.下列判断正确的是()①若一个平面内有两条直线与另一个平面平行,则这两个平面平行;②若一个平面内有无数条直线与另一个平面平行,则这两个平面平行;③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.A.①③B.②④C.②③④D.③④解析:①②中两个平面可以相交;③是两个平面平行的定义;④是两个平面平行的判定定理,故选D.答案:D2.使平面α∥平面β的一个条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,aα,a∥βC.存在两条平行直线a,b,aα,bβ,a∥β,b∥αD.α内存在两条相交直线a,b分别平行于β内两条直线解析:A,B,C中的条件都不一定使α∥β,反例分别为图①②③(图中a∥l,b∥l);D正确,因为a∥β,b∥β,又a,b相交,从而α∥β.答案:D3.如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点,则EF与平面BB1D1D的位置关系是()A.平行B.相交C.面内D.无法判断解析:连接A1C1,设A1C1∩B1D1=O,连接OB(图略),显然OB∥EF,根据线面平行的判定定理可知,EF∥平面BB1D1D,故选A.答案:A4.如图,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFGH,且四边形EFGH是矩形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是菱形D.EH∥平面ADC,且四边形EFGH是梯形解析:∵AE∶EB=AF∶FD=1∶4,∴EF∥BD且EF=BD.又H,G分别为BC,CD的中点,∴HG綊BD.∴EF∥HG且EF≠HG.∴四边形EFGH为梯形.∵BD平面BCD且EF⃘平面BCD.∴EF∥平面BCD.答案:B二、填空题(每小题5分,共10分)5.如图所示的四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是________.(填序号)解析:①中连接点A与点B上面的顶点,记为C,则易证平面ABC∥平面MNP,所以AB∥平面MNP;④中AB∥NP,根据空间直线与平面平行的判定定理可以得出AB∥平面MNP;②,③中,AB均与平面MNP相交.答案:①④6.已知点S是正三角形ABC所在平面外一点,点D,E,F分别是SA,SB,SC的中点,则平面DEF与平面ABC的位置关系是________.解析:由D,E,F分别是SA,SB,SC的中点,知EF是△SBC的中位线,∴EF∥BC.又∵BC平面ABC,EF⃘平面ABC,∴EF∥平面ABC.同理DE∥平面ABC.又∵EF∩DE=E,∴平面DEF∥平面ABC.答案:平行三、解答题(每小题10分,共20分)7.如图,在直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点,求证:AC1∥平面CDB1.证明:如图,连接BC1,设BC1与B1C的交点为E,连接DE.∴D是AB的中点,E是BC1的中点,∴DE∥AC1.∵DE平面CDB1,AC1⃘平面CDB1,∴AC1∥平面CDB1.8.P为正方形ABCD所在平面外一点,E,F,G分别为PD,AB,DC的中点,如图.求证:(1)AE∥平面PCF;(2)平面PCF∥平面AEG.证明:(1)取PC中点H,分别连接EH,FH.∵E,F,H分别为PD,AB,PC的中点,∴EH綊DC,AF綊DC.∴EH綊AF.∴EAFH为平行四边形.∴EA∥FH.又AE⃘平面PCF,FH平面PCF,∴AE∥平面PCF.(2)∵E,G分别为PD,CD的中点,∴EG∥PC.又EG⃘平面PCF,PC平面PCF,∴EG∥平面PCF.由(1)知AE∥平面PCF,EG∩AE=E.∴平面PCF∥平面AEG.☆☆☆9.(10分)如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?请说明理由.解析:当Q为CC1的中点时,平面D1BQ∥平面PAO.证明如下:∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.连接DB,∵P,O分别为DD1,DB的中点,∴D1B∥PO.又D1B⃘平面PAO,QB⃘平面PAO,∴D1B∥平面PAO,QB∥平面PAO,又D1B∩QB=B,∴平面D1BQ∥平面PAO.