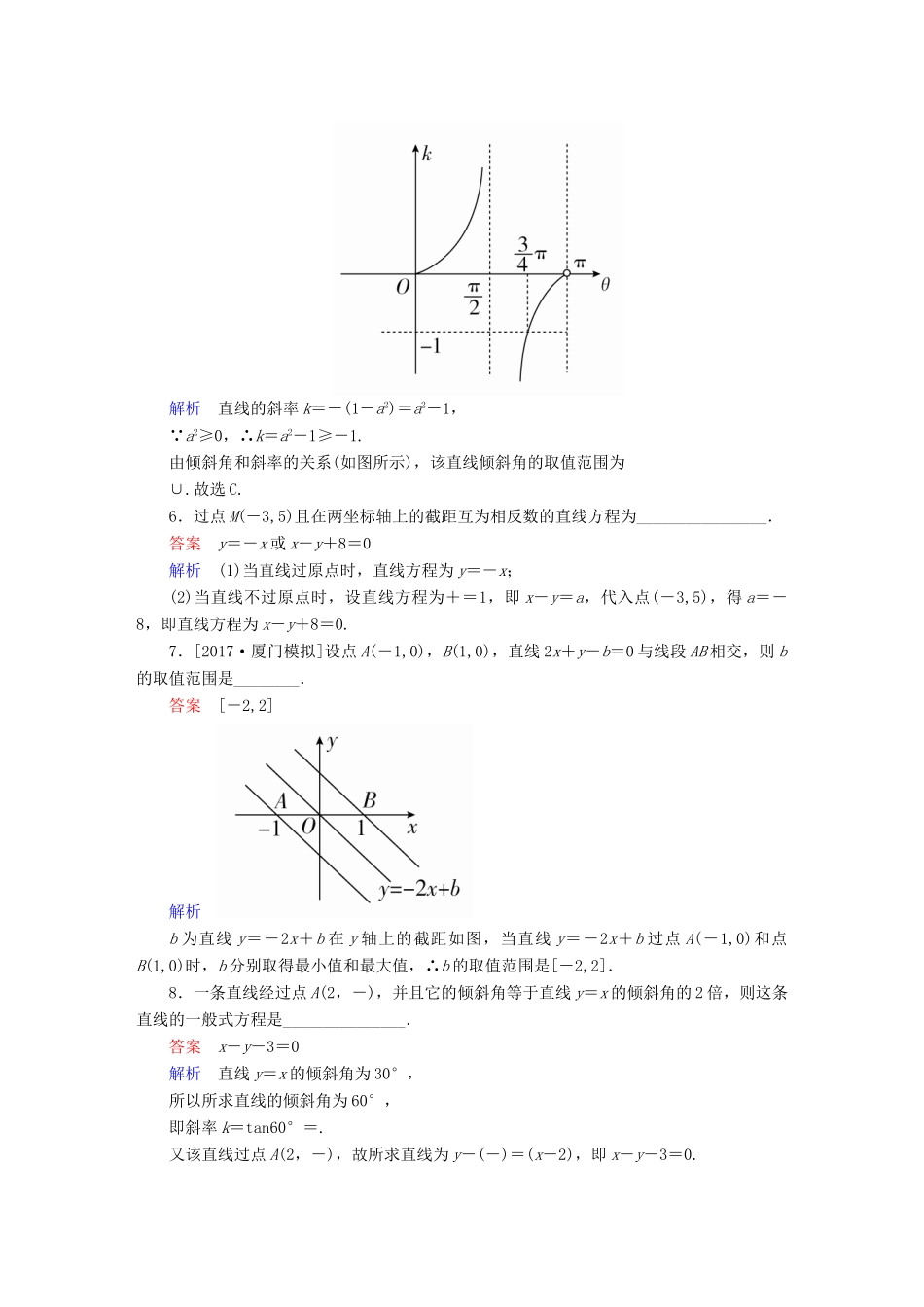
2018版高考数学一轮总复习第8章平面解析几何8.1直线的倾斜角与斜率、直线的方程模拟演练文[A级基础达标](时间:40分钟)1.[2017·安徽模拟]直线l:xsin30°+ycos150°+1=0的斜率是()A.B.C.-D.-答案A解析设直线l的斜率为k,则k=-=.2.若经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为,则y等于()A.-1B.-3C.0D.2答案B解析由k==tan=-1,得-4-2y=2,所以y=-3.3.[2017·沈阳模拟]直线ax+by+c=0同时要经过第一、第二、第四象限,则a,b,c应满足()A.ab>0,bc<0B.ab>0,bc>0C.ab<0,bc>0D.ab<0,bc<0答案A解析由于直线ax+by+c=0经过第一、二、四象限,所以直线存在斜率,将方程变形为y=-x-.易知-<0且->0,故ab>0,bc<0.4.若直线ax+by=ab(a>0,b>0)过点(1,1),则该直线在x轴,y轴上的截距之和的最小值为()A.1B.2C.4D.8答案C解析 直线ax+by=ab(a>0,b>0)过点(1,1),∴a+b=ab,即+=1,∴a+b=(a+b)=2++≥2+2=4,当且仅当a=b=2时上式等号成立.∴直线在x轴,y轴上的截距之和的最小值为4.5.直线(1-a2)x+y+1=0的倾斜角的取值范围是()A.B.C.∪D.∪答案C解析直线的斜率k=-(1-a2)=a2-1, a2≥0,∴k=a2-1≥-1.由倾斜角和斜率的关系(如图所示),该直线倾斜角的取值范围为∪.故选C.6.过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为________________.答案y=-x或x-y+8=0解析(1)当直线过原点时,直线方程为y=-x;(2)当直线不过原点时,设直线方程为+=1,即x-y=a,代入点(-3,5),得a=-8,即直线方程为x-y+8=0.7.[2017·厦门模拟]设点A(-1,0),B(1,0),直线2x+y-b=0与线段AB相交,则b的取值范围是________.答案[-2,2]解析b为直线y=-2x+b在y轴上的截距如图,当直线y=-2x+b过点A(-1,0)和点B(1,0)时,b分别取得最小值和最大值,∴b的取值范围是[-2,2].8.一条直线经过点A(2,-),并且它的倾斜角等于直线y=x的倾斜角的2倍,则这条直线的一般式方程是_______________.答案x-y-3=0解析直线y=x的倾斜角为30°,所以所求直线的倾斜角为60°,即斜率k=tan60°=.又该直线过点A(2,-),故所求直线为y-(-)=(x-2),即x-y-3=0.9.已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:(1)过定点A(-3,4);(2)斜率为.解(1)设直线l的方程为y=k(x+3)+4,它在x轴,y轴上的截距分别是--3,3k+4,由已知,得(3k+4)=±6,解得k1=-或k2=-.故直线l的方程为2x+3y-6=0或8x+3y+12=0.(2)设直线l在y轴上的截距为b,则直线l的方程是y=x+b,它在x轴上的截距是-6b,由已知,得|-6b·b|=6,∴b=±1,∴直线l的方程为x-6y+6=0或x-6y-6=0.10.已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.解解法一:直线x+my+m=0恒过点A(0,-1),kAP==-2,kAQ==,当m≠0时,则-≥或-≤-2.∴-≤m≤且m≠0.又m=0时,直线x+my+m=0与线段PQ有交点,∴所求m的取值范围是.解法二:过P、Q两点的直线方程为y-1=(x+1),即y=x+,代入x+my+m=0,整理得x=-,由已知-1≤-≤2,解得-≤m≤,即m的取值范围是.[B级知能提升](时间:20分钟)11.在等腰三角形AOB中,AO=AB,点O(0,0),A(1,3),点B在x轴的正半轴上,则直线AB的方程为()A.y-1=3(x-3)B.y-1=-3(x-3)C.y-3=3(x-1)D.y-3=-3(x-1)答案D解析因为AO=AB,所以直线AB的斜率与直线AO的斜率互为相反数,所以kAB=-kOA=-3,所以直线AB的点斜式方程为:y-3=-3(x-1).12.[2017·大庆模拟]两直线-=a与-=a(其中a为不为零的常数)的图象可能是()答案B解析直线方程-=a可化为y=x-na,直线-=a可化为y=x-ma,由此可知两条直线的斜率同号.13.若ab>0,且A(a,0),B(0,b),C(-2,-2)三点共线,则ab的最小值为________.答案16解析根据A(a,0),B(0,b)确定直线的方程为+=1,又C(-2,-2)在该直线上,故+=1,所以-2(a+b)=ab.又ab>0,故a<0,b<0.根据基本(均值)不等式ab=-2(a+b)≥4,从而≤...