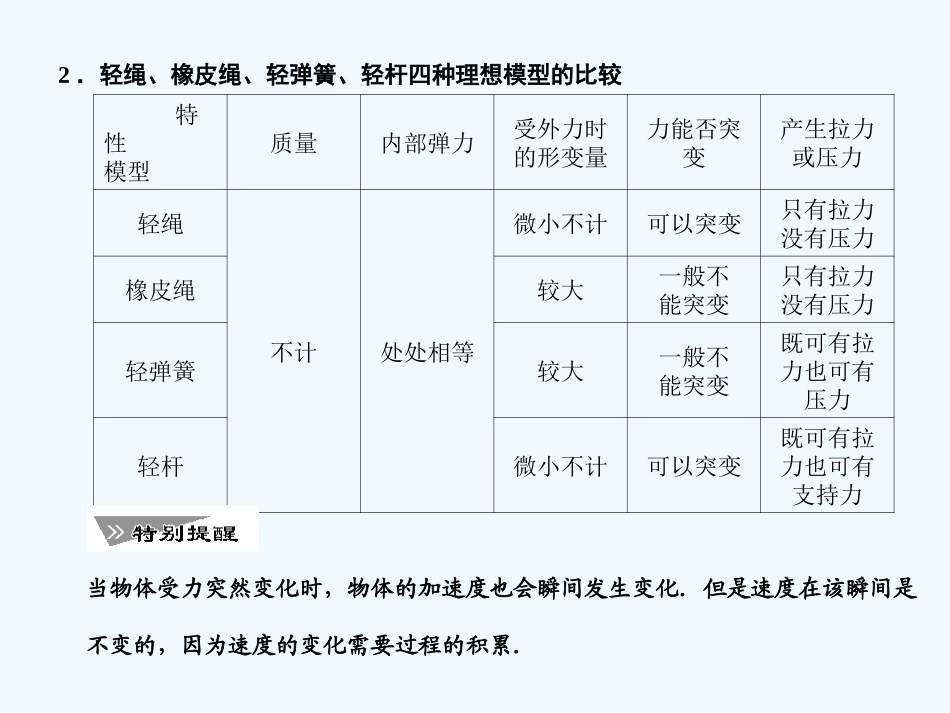
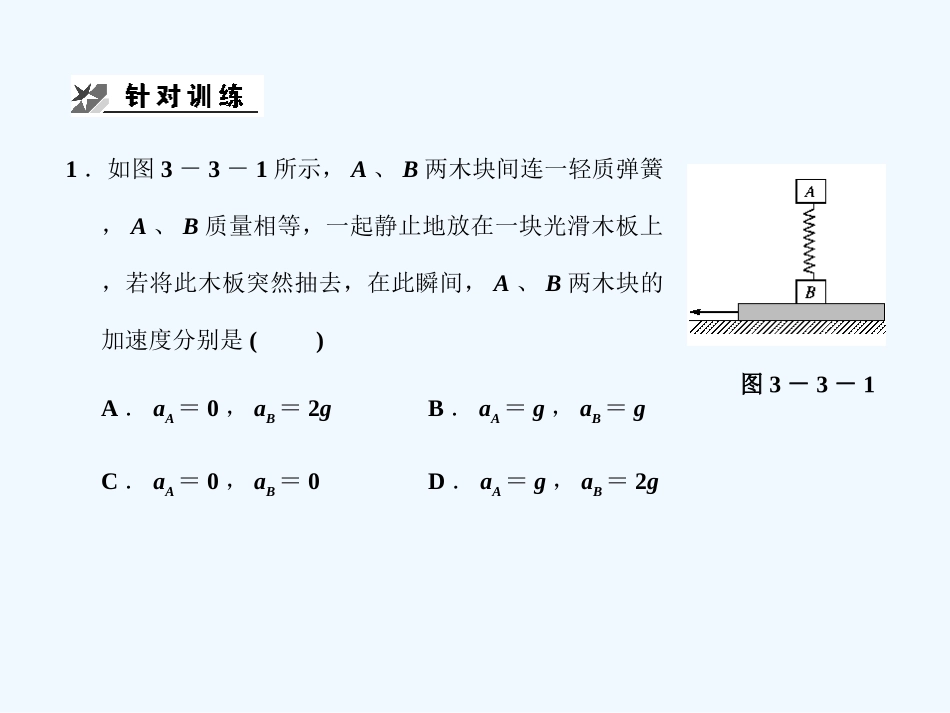
一、瞬时加速度问题1.a与F合的瞬时对应关系物体在每一瞬时的加速度只决定于这一瞬时的合力,而与这一瞬时之前或之后的合外力没有关系.第3课时专题牛顿运动定律的综合应用2.轻绳、橡皮绳、轻弹簧、轻杆四种理想模型的比较特性模型质量内部弹力受外力时的形变量力能否突变产生拉力或压力轻绳不计处处相等微小不计可以突变只有拉力没有压力橡皮绳较大一般不能突变只有拉力没有压力轻弹簧较大一般不能突变既可有拉力也可有压力轻杆微小不计可以突变既可有拉力也可有支持力当物体受力突然变化时,物体的加速度也会瞬间发生变化.但是速度在该瞬间是不变的,因为速度的变化需要过程的积累.1.如图3-3-1所示,A、B两木块间连一轻质弹簧,A、B质量相等,一起静止地放在一块光滑木板上,若将此木板突然抽去,在此瞬间,A、B两木块的加速度分别是()A.aA=0,aB=2gB.aA=g,aB=gC.aA=0,aB=0D.aA=g,aB=2g图3-3-1解析:由题意得:当刚抽去木板时,弹簧还没有来得及恢复形变,所以弹力的大小不变,仍等于物体A的重力大小,对于物体B,受到的力为竖直向下的重力和弹簧竖直向下的弹力的作用,根据牛顿第二定律得到物体B的加速度大小为2g.而对物体A,进行受力分析得:受到竖直向下的重力和弹簧竖直向上的弹力作用,两力不变,合力为零,根据牛顿第二定律得加速度为零,综上所述,本题的正确选项为A.答案:A二、临界与极值问题在应用牛顿运动定律解决动力学问题中,当物体运动的加速度不同时,物体有可能处于不同的状态,特别是题目中出现“最大”、“最小”、“刚好”等词语时,往往会有临界现象,此时要采用假设法或极限分析法,看物体在不同的加速度时,会有哪些现象发生,尽快找出临界点,求出临界条件.1.“假设法”分析动力学问题假设法是解物理问题的一种重要方法,用假设法解题,一般依题意从某一假设入手,然后运用物理规律得出结果,再进行适当讨论,从而找出正确答案,这样解题科学严谨、合乎逻辑,而且可以拓宽思路,最常见的是用假设法判定力的方向.方法一:首先假定某力不存在,看物体发生怎样的运动,然后再确定该力应在什么方向物体才会产生题目给定的运动状态.方法二:假定某力沿某一方向,用运动规律进行验算,若算得正值,说明此力与假定的方向相同,否则相反.方法三:在力的作用线上定出坐标轴的正方向,将此力用正号运算,若求得的是正值,说明此力与坐标轴同向,否则相反.2.“极限法”分析动力学问题在物体的运动状态变化过程中,往往达到某个特定状态时,有关的物理量将发生突变,此状态叫临界状态.相应的待求物理量的值叫临界值.利用临界值来作为解题思路的起点是一种很有用的思考途径,也可以说是利用临界条件求解.这类问题的关键在于抓住满足临界值的条件,准确地分析物理过程,进行求解.2.如图3-3-2所示,质量都为m的A、B两物体叠放在竖直弹簧上并保持静止,用大小等于mg的恒力F向上拉B,运动距离h时B与A分离.则下列说法中正确的是()A.B和A刚分离时,弹簧为原长B.B和A刚分离时,它们的加速度为gC.弹簧的劲度系数等于mg/hD.在B与A分离之前,它们做匀加速运动解析:在施加外力F前,对A、B整体受力分析可得:2mg=kx1,A、B两物体分离时,B物体受力平衡,两者加速度恰好为零,选项A、B错误;对物体A:mg=kx2,由于x1-x2=h,所以弹簧的劲度系数为k=mg/h,选项C正确;在B与A分离之前,由于弹簧弹力逐渐减小,加速度逐渐减小,选项D错误.答案:C三、整体法与隔离法选取的原则系统问题是指在外力作用下几个物体连在一起运动的问题,系统内的物体的加速度可以相同,也可以不相同,对该类问题处理方法如下:1.隔离法的选取(1)适应情况:若系统内各物体的加速度不相同,且需要求物体之间的作用力.(2)处理方法:把物体从系统中隔离出来,将内力转化为外力,分析物体的受力情况和运动情况,并分别应用牛顿第二定律列方程求解,隔离法是受力分析的基础,应重点掌握.2.整体法的选取(1)适应情况:若系统内各物体具有相同的加速度,且不需要求物体之间的作用力.(2)处理方法:把系统内各物体看成一个整体(当成一个质点)来分析整体受到的外...