【数学】152定积分课件（苏教版选修2-2）VIP免费

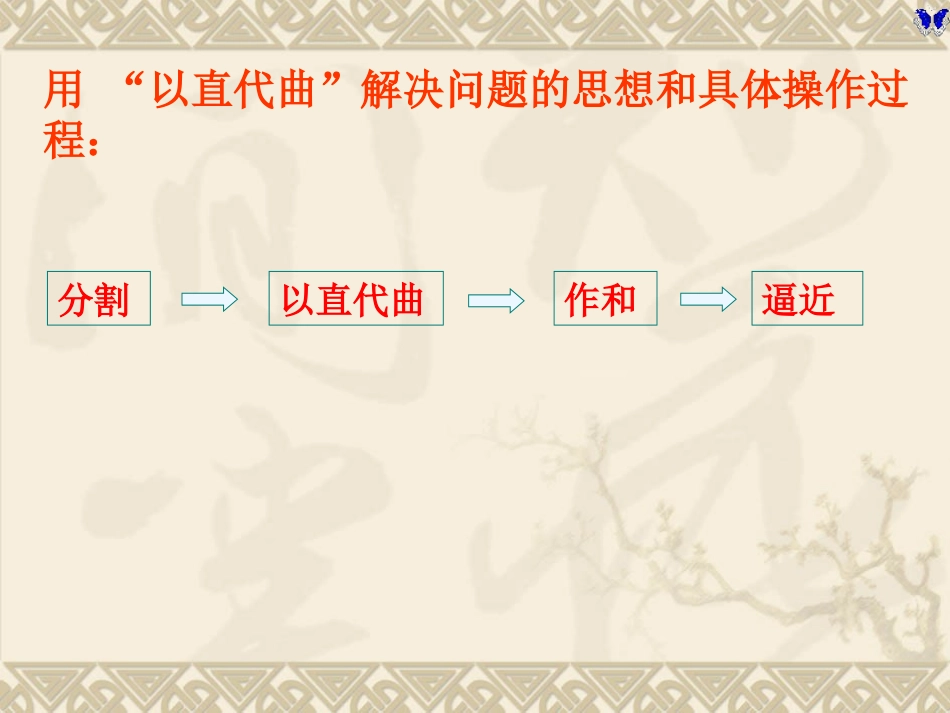
第1章导数及其应用1.5.2定积分微积分在几何上有两个基本问题1.如何确定曲线上一点处切线的斜率；2.如何求曲线下方“曲线梯形”的面积。xy0xy0xyo直线几条线段连成的折线曲线？知识回顾：用“以直代曲”解决问题的思想和具体操作过程：分割以直代曲作和逼近求由连续曲线y=f(x)对应的曲边梯形面积的方法(2)以直代曲:任取xi[xi-1,xi]，第i个小曲边梯形的面积用高为f(xi),宽为Dx的小矩形面积f(xi)Dx近似地去代替.(4)逼近:所求曲边梯形的面积S为(3)作和:取n个小矩形面积的和作为曲边梯形面积S的近似值：xi-1y=f(x)xyObaxixix10,()()niixfxSn1()niiSfx(1)分割:在区间[a,b]上等间隔地插入n-1个点,将它等分成n个小区间:每个小区间宽度⊿xban11211,,,,,,,,,iinaxxxxxxb11()()nnniiiibaSfxxfxn小矩形面积和如果当n+∞时，Sn就无限接近于某个常数，这个常数为函数f(x)在区间[a,b]上的定积分，记作baf(x)dx，即baf(x)dxni10limf(i)xi。从求曲边梯形面积S的过程中可以看出,通过“四个步骤”:分割---以直代曲----求和------逼近.定积分的定义:一般地,设函数f(x)在区间[a,b]上有定义,将区间[a,b]等分成n个小区间,每个小区的长度为,在每个小区间上取一点,依次为x1,x2,…….xi,….xn,作和如果无限趋近于0时,Sn无限趋近于常数S,那么称常数S为函数f(x)在区间[a,b]上的定积分,记作:.)(nabxxx)f(xx)f(xx)x(fSn21nbaSf(x)dxx定积分的相关名称：———叫做积分号，f(x)dx—叫做被积表达式，f(x)——叫做被积函数,x———叫做积分变量，a———叫做积分下限，b———叫做积分上限，[a,b]—叫做积分区间。()baSfxdx被积函数被积表达式积分变量积分下限积分上限()baSfxdxSbaf(x)dx；按定积分的定义，有(1)由连续曲线y=f(x)(f(x)0)，直线x=a、x=b及x轴所围成的曲边梯形的面积为(2)设物体运动的速度v=v(t)，则此物体在时间区间[a,b]内运动的距离s为();baSvtdt(3)设物体在变力F=F(r)的方向上有位移，则F在位移区间[a,b]内所做的功W为().baWFrdr注：定积分数值只与被积函数及积分区间[a,b]有关,与积分变量记号无关bababaduufdttfdxxf)()()(例1（1).由曲线y=x2+1与直线x=1,x=3及x轴所围成的曲边梯形的面积,用定积分表示为____________.223sintdt(2).中,积分上限是___,积分下限是___,积分区间是______dxx)1(2312-2[-2,2](3).定积分=__________.211)dx(x25定积分的几何意义.当f(x)≥0，定积分badxxf)(的几何意义就是bAoxyay=f(x)S曲线y=f(x)直线x=a，x=b，y=0所围成的曲边梯形的面积baSf(x)dx:即思考:函数在区间[a,b]上的定积分能否为负的?当函数f(x)0，x[a,b]时定积分几何意义badxxf)(Sdxxfba)(即就是位于x轴下方的曲边梯形面积的相反数.oxyaby=f(x)S当函数f(x)在x[a,b]有正有负时,定积分几何意义badxxf)(321baSSSf(x)dx即就是图中几个曲边图形面积的代数和,(x轴上方面积取正号,x轴下方面积取负号)OXS2S1yS3定积分的几何意义：在区间[a,b]上曲线与x轴所围成图形面积的代数和(即x轴上方的面积减去x轴下方的面积).50(24)xdx计算定积分-465OxyAB50(24)945xdx例2解析：如图所示，计算可得A的面积是9，B的面积是4，从而定积分的基本性质性质1.dx)]x(g)x(f[bababadx)x(gdx)x(f性质2.badx)x(kfbadx)x(fk课外拓展定积分的基本性质定积分关于积分区间具有可加性bccabadx)x(fdx)x(fdx)x(f性质3.2121ccbccabadx)x(fdx)x(fdx)x(fdx)x(fOxyabyf(x)Ｃ小结:１．定积分的实质：特殊和式的逼近值．２．定积分的思想和方法：分割化整为零求和积零为整取逼近精确值——定积分求近似以直（不变）代曲（变）取逼近3.定积分的几何意义及简单应用