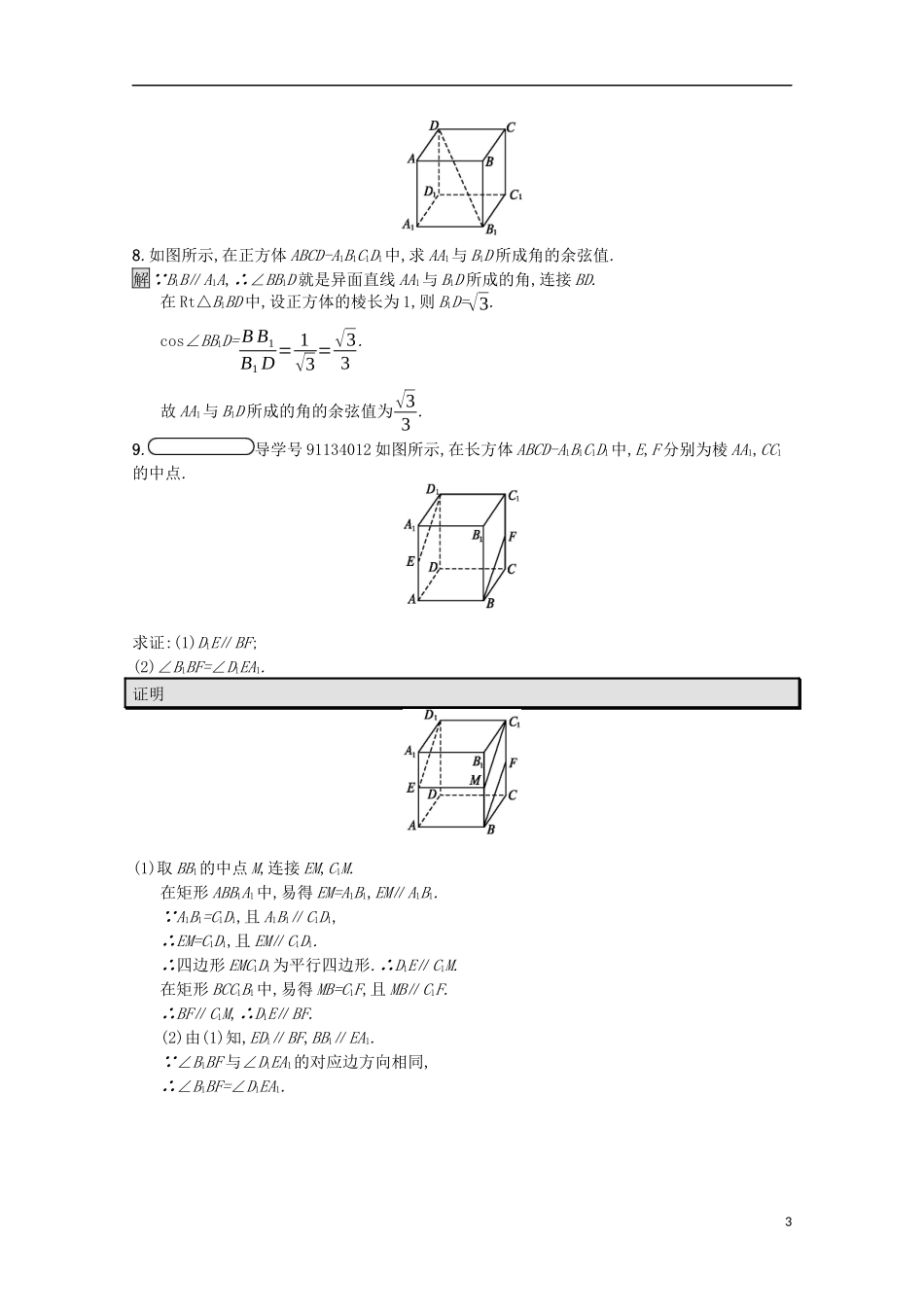
第2课时等角定理与异面直线所成的角课后篇巩固探究1.如图,在三棱柱ABC-A1B1C1中,E,F,G分别为棱A1C1,B1C1,B1B的中点,则∠EFG与∠ABC1()A.相等B.互补C.相等或互补D.不确定解析因为E,F,G分别为A1C1,B1C1,BB1的中点,所以EF∥A1B1∥AB,FG∥BC1,所以∠EFG与∠ABC1的两组对应边分别平行,一组对应边方向相同,另一组对应边方向相反,故∠EFG与∠ABC1互补.答案B2.若BD1是正方体ABCD-A1B1C1D1的一条体对角线,则这个正方体中面对角线与BD1异面的共有()A.7条B.6条C.4条D.3条解析正方体的六个面中各有一条对角线符合题意.答案B3.若OA∥O'A',OB∥O'B',且∠AOB=130°,则∠A'O'B'为()A.130°B.50°C.130°或50°D.不能确定解析根据定理,∠A'O'B'与∠AOB相等或互补,即∠A'O'B'=130°或∠A'O'B'=50°.答案C4.分别和两条异面直线平行的两条直线的位置关系是()A.一定平行B.一定相交C.一定异面D.相交或异面解析画出图形,得到结论.如图(1),分别与异面直线a,b平行的两条直线c和d是相交关系.如图(2),分别与异面直线a,b平行的两条直线c和d是异面关系.综上可知,应选D.答案D5.在四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为()A.90°B.45°C.60°D.30°解析1设G为AD的中点,连接GF,GE,则GF,GE分别为△ABD,△ACD的中位线.故GF∥AB,且GF=12AB=1,GE∥CD,且GE=12CD=2,∠GEF就是异面直线EF与CD所成的角.∵EF⊥AB,∴EF⊥GF,∴△GEF为直角三角形,且sin∠GEF=12,∴∠GEF=30°.故选D.答案D6.如图,在长方体ABCD-A1B1C1D1中,判断下列直线的位置关系:(1)直线A1B与直线D1C的位置关系是;(2)直线A1B与直线B1C的位置关系是;(3)直线D1D与直线D1C的位置关系是;(4)直线AB与直线B1C的位置关系是.解析(1)在长方体ABCD-A1B1C1D1中,A1D1∥BC,所以四边形A1BCD1为平行四边形,所以A1B∥D1C.(2)直线A1B与直线B1C不同在任何一个平面内.(3)直线D1D与直线D1C相交于点D1.(4)直线AB与直线B1C不同在任何一个平面内.答案(1)平行(2)异面(3)相交(4)异面7.如图所示,在长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E,F,G分别是DD1,AB,CC1的中点,则异面直线A1E与GF所成的角是.解析连接GB1,B1F,则GB1∥A1E,故∠B1GF或其补角即为A1E与GF所成的角,B1G=√C1B12+C1G2=√12+12=√2,B1F=√B1B2+BF2=√22+12=√5,GF=√CG2+CB2+BF2=√3,∴B1G2+FG2=B1F2,∴∠B1GF=90°.答案90°28.如图所示,在正方体ABCD-A1B1C1D1中,求AA1与B1D所成角的余弦值.解∵B1B∥A1A,∴∠BB1D就是异面直线AA1与B1D所成的角,连接BD.在Rt△B1BD中,设正方体的棱长为1,则B1D=√3.cos∠BB1D=BB1B1D=1√3=√33.故AA1与B1D所成的角的余弦值为√33.9.导学号91134012如图所示,在长方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点.求证:(1)D1E∥BF;(2)∠B1BF=∠D1EA1.证明(1)取BB1的中点M,连接EM,C1M.在矩形ABB1A1中,易得EM=A1B1,EM∥A1B1.∵A1B1=C1D1,且A1B1∥C1D1,∴EM=C1D1,且EM∥C1D1.∴四边形EMC1D1为平行四边形.∴D1E∥C1M.在矩形BCC1B1中,易得MB=C1F,且MB∥C1F.∴BF∥C1M,∴D1E∥BF.(2)由(1)知,ED1∥BF,BB1∥EA1.∵∠B1BF与∠D1EA1的对应边方向相同,∴∠B1BF=∠D1EA1.34