高中高考数学3月模拟考试试题04-人教版高三全册数学试题VIP专享VIP免费

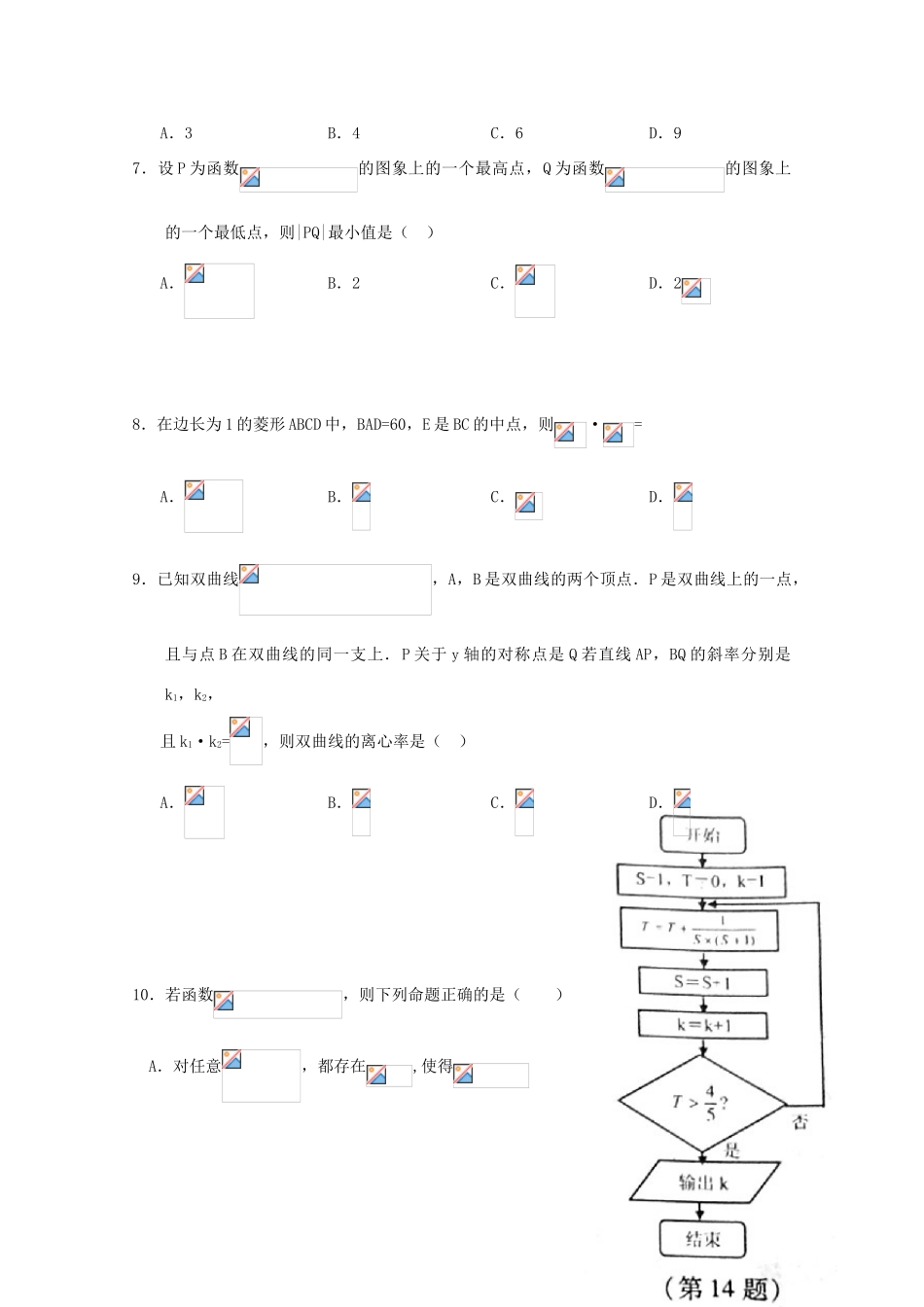
江门市普通高中2017届高考高三数学3月模拟考试试题(四)一、选择题（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的）1．设全集U=R，集合则A．B．C．D．2．已知i是虚数单位，则（）A．B．C．D．3．设，则“”直线与圆恰好有一个公共点”的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4．在一盆子中号为1，2的红色球个，编号为1，2的白色球2个，现从盒子中摸出两个球，每个球被摸到的概率相同，则摸出的两个球中既含有2种不同颜色又含有2个不同编号的概率是A．B．C．D．5．设m，n是两条不同的直线，是两个不同的半面A．若m∥，n∥，m∥n，则∥B．若m∥，n∥，∥则m∥nC．若m⊥，n⊥，m⊥n则⊥D．若m⊥，n⊥，⊥则m⊥n6．已知实数x，y满足不等式组则的最小值是A．3B．4C．6D．97．设P为函数的图象上的一个最高点，Q为函数的图象上的一个最低点，则|PQ|最小值是（）A．B．2C．D．28．在边长为1的菱形ABCD中，BAD=60，E是BC的中点，则·=A．B．C．D．9．已知双曲线，A，B是双曲线的两个顶点．P是双曲线上的一点，且与点B在双曲线的同一支上．P关于y轴的对称点是Q若直线AP，BQ的斜率分别是k1，k2，且k1·k2=，则双曲线的离心率是（）A．B．C．D．10．若函数，则下列命题正确的是（）A．对任意，都存在,使得B．对任意，都存在，使得C．对任意，都存在，使得D．对任意，都存在，使得二、填空题（本大题共7小题，每小题4分，共28分）11．函数的定义域是。12．已知，则。13．已知数列{an}中a3=7，a7=3，且是等差数列，则a10=。14．若某程序框图如图所示，则该程序运行后输出的值是____。15．一个空间几何体的三视图如图所示，则该几何体的表面积为。16．在△OAB中，C为OA上的一点，且是BC的中点，过点A的直线∥OD，P是直线上的任意点，若则=。17．设a，b是关于x的方程的两个实根（），直线过点A（a，a2），B（b，b2），则坐标原点O到直线的距离是____。三、解答题（本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤）18．（本题满分14分）在△ABC中，角A、B、C所对的边分别为a,b，c．已知c=2．acosB－bcosA=。（I）求bcosA的值；（Ⅱ）若a=4．求△ABC的面积。19．（本小题满分14分）在各项均为正数的等比数列{an}中，a2=2，2a3，a5，3a4成等差数列，数列{bn}满足bn=21og2an+1。（I）求数列{an}的通项公式；（II）设Sn为数列{bn}的前n项和，数列{cn}满足。当cn最大时，求n的值。20．（本题满分15分）在几何体中，AA1⊥平面ABC，AB⊥BC，CC1∥AA1，AB=BCAA1=2，CC1=1，D，E分别是AB，AA1的中点。（Ⅰ）求证：BC1∥平面CDE；（Ⅱ）求二面角E—DC—A的平面的正切值。21．（本题满分15分）已知函数。（I）当a=1时，求过点P（－1，0）且曲线y=f（x）相切的直线方程；（Ⅱ）当时，不等式恒成立，求a的取值集合。22．（本题满分14分）已知直线y=2x－2与抛物线x2=2py（p>0）交于M1，M2两点，|M1M2|=。（I）求P的值；（Ⅱ）设A是直线y=上一点，直线AM2交抛物线于另点M3，直线M1M3交直线y=于点B，求·的值。参考答案一、选择题(本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的)：题号12345678910答案BDACCBCDCB二、填空题(本大题共7小题，每小题4分，共28分)：11.12.13.14.615.16.17.2三、解答题（本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤）18.(本题满分14分)(Ⅰ) ，根据余弦定理得，，∴，又 ，∴，∴.7分(Ⅱ)由及，得.又 ，∴，∴，∴.14分19.(本题满分14分)(Ⅰ)设等比数列的公比为， ，，成等差数列，∴，即，∴或(舍去).又，则，即数列的通项公式为.7分(Ⅱ)，则是等差数列，，则，， 当时，，当时，，∴取最大值时，的值是4和5.14分20.(本题满分15分)(Ⅰ)连接ACR1R交EC于点F，由题意知四边形ACCR1RE是矩形，则F是ACR1R的中点，连接DF， D是AB的中点，∴DF是△ABCR1R的中位线，∴BCR1R//DF，4分 BCR1R平面EDC，DF平面EDC，∴BCR1R//平面CDE.7分(Ⅱ)作AH⊥直线CD，垂足为H，连接HE， AAR1R⊥平面ABC，∴AAR1R⊥DC，∴CD⊥平面AHE，...