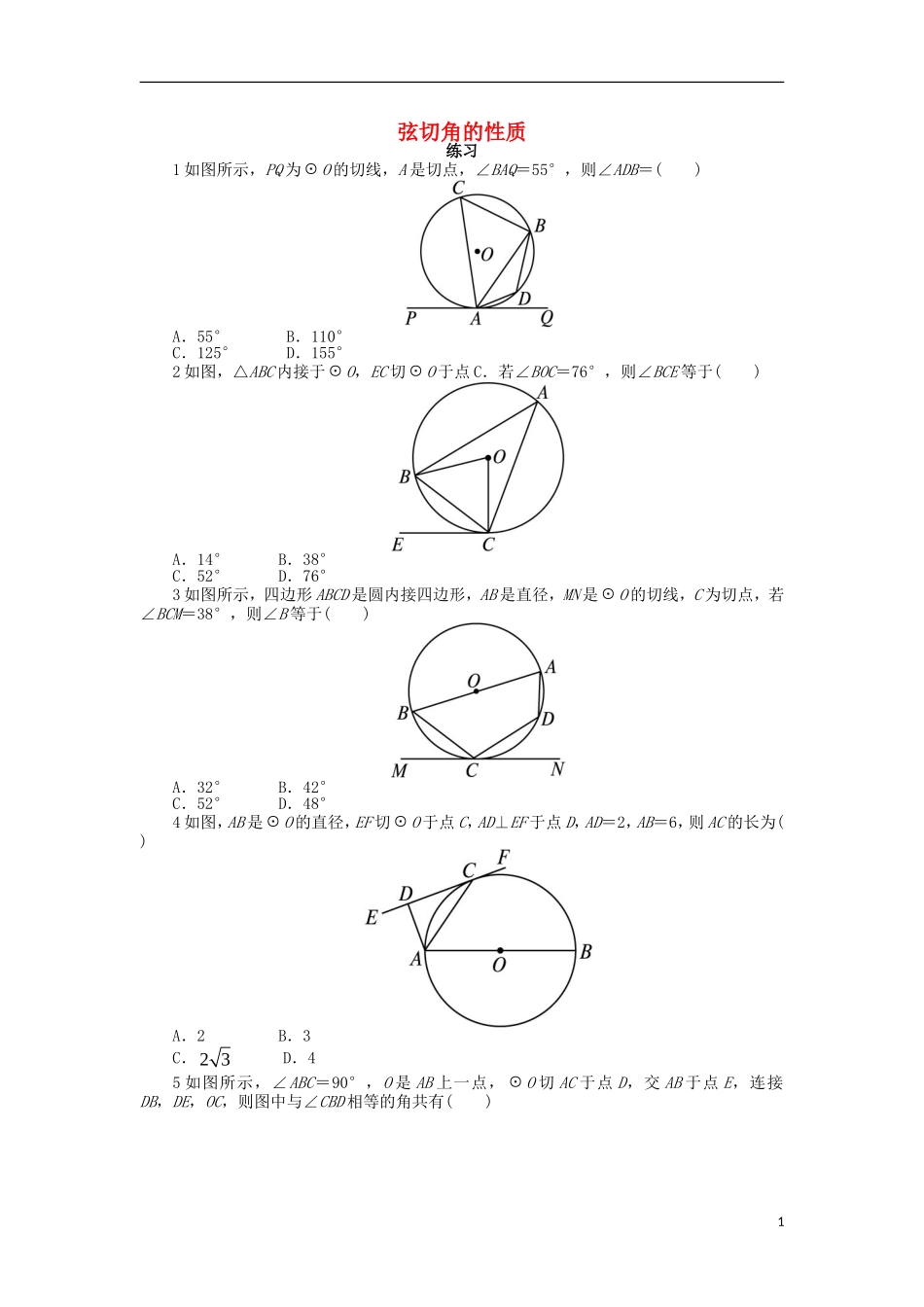
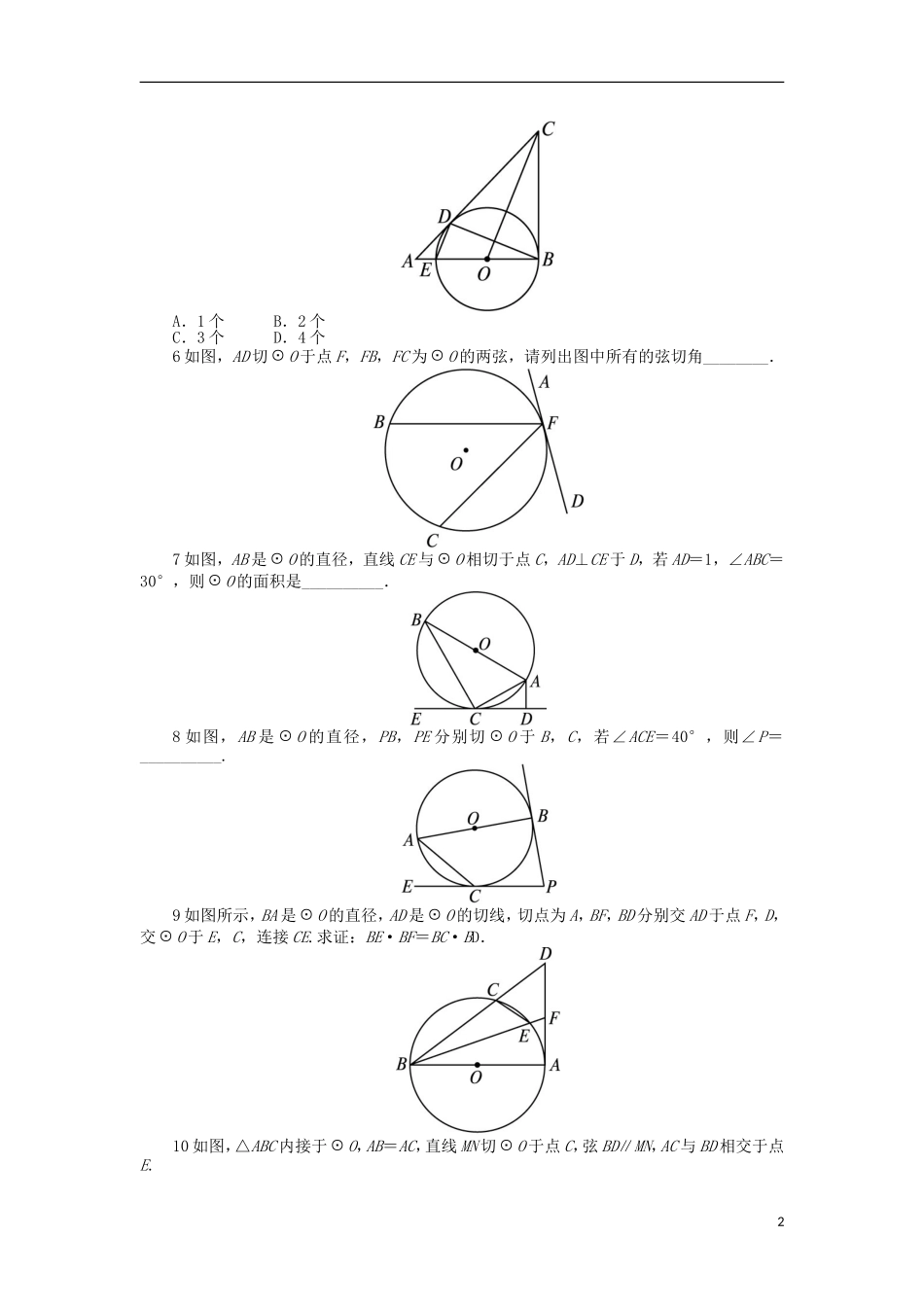
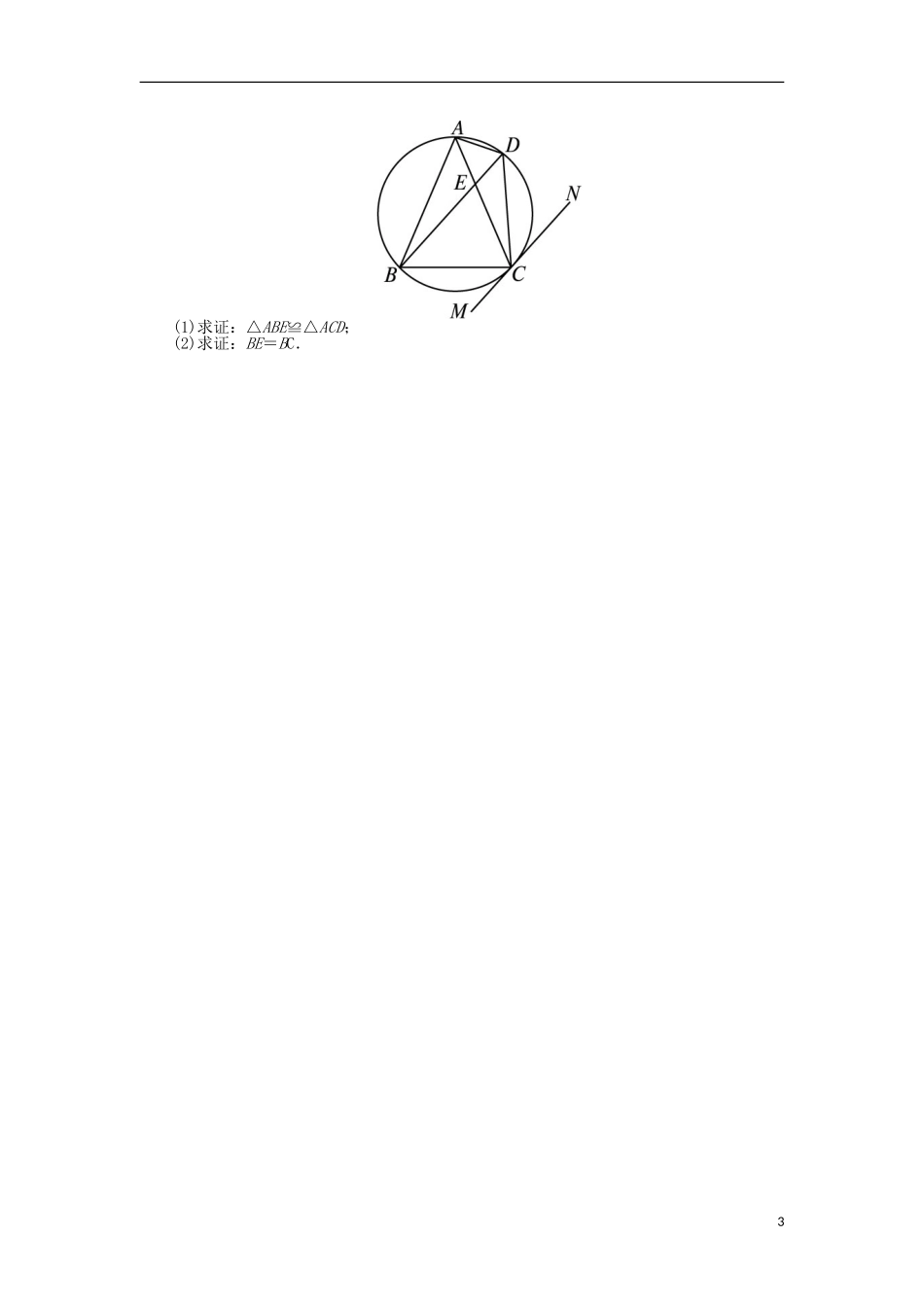
弦切角的性质练习1如图所示,PQ为O的切线,A是切点,∠BAQ=55°,则∠ADB=()A.55°B.110°C.125°D.155°2如图,△ABC内接于O,EC切O于点C.若∠BOC=76°,则∠BCE等于()A.14°B.38°C.52°D.76°3如图所示,四边形ABCD是圆内接四边形,AB是直径,MN是O的切线,C为切点,若∠BCM=38°,则∠B等于()A.32°B.42°C.52°D.48°4如图,AB是O的直径,EF切O于点C,AD⊥EF于点D,AD=2,AB=6,则AC的长为()A.2B.3C.23D.45如图所示,∠ABC=90°,O是AB上一点,O切AC于点D,交AB于点E,连接DB,DE,OC,则图中与∠CBD相等的角共有()1A.1个B.2个C.3个D.4个6如图,AD切O于点F,FB,FC为O的两弦,请列出图中所有的弦切角________.7如图,AB是O的直径,直线CE与O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则O的面积是__________.8如图,AB是O的直径,PB,PE分别切O于B,C,若∠ACE=40°,则∠P=__________.9如图所示,BA是O的直径,AD是O的切线,切点为A,BF,BD分别交AD于点F,D,交O于E,C,连接CE.求证:BE·BF=BC·BD.10如图,△ABC内接于O,AB=AC,直线MN切O于点C,弦BD∥MN,AC与BD相交于点E.2(1)求证:△ABE≌△ACD;(2)求证:BE=BC.3参考答案1答案:C∵PQ是切线,∴∠C=∠BAQ=55°.又∵四边形ADBC内接于圆,∴∠ADB=180°-∠C=180°-55°=125°.2答案:B∵EC为O的切线,∴∠BCE=∠BAC=12∠BOC=38°.3答案:C连接AC,如图所示.∵MN切圆于C,BC是弦,∴∠BAC=∠BCM.∵AB是直径,∴∠ACB=90°.∴∠B+∠BAC=90°.∴∠B+∠BCM=90°,∴∠B=90°-∠BCM=52°.4答案:C连接BC,如图所示.∵EF是O的切线,∴∠ACD=∠ABC.又AB是O的直径,∴∠ACB=90°.又AD⊥EF,∴∠ACB=∠ADC.∴△ADC∽△ACB.∴ABACACAD.∴AC2=AD·AB=2×6=12,∴AC=23.5答案:C∵AB⊥BC,∴BC与O相切,BD为弦.∴∠CBD=∠BED.同理可得∠CDB=∠BED,∴∠CBD=∠CDB.连接OD.∵OD=OB,OC=OC,∴Rt△COD≌Rt△COB.∴CB=CD,∠DCO=∠BCO.∴OC⊥BD.又DE⊥BD,∴DE∥OC.∴∠BED=∠BOC,∴∠CBD=∠BOC.∴与∠CBD相等的角共有3个.6答案:∠AFB,∠AFC,∠DFC,∠DFB7答案:4π∵DE是切线,∴∠ACD=∠ABC=30°.又AD⊥CD,∴AC=2AD=2.又∵AB是直径,∴∠ACB=90°.又∠ABC=30°,∴AB=2AC=4,4∴OA=12AB=2.∴O的面积为S=π·OA2=4π.8答案:80°如图所示,连接BC,则∠ACE=∠ABC,∠ACB=90°.又∠ACE=40°,则∠ABC=40°.所以∠BAC=90°-∠BCA=90°-40°=50°,∠ACP=180°-∠ACE=140°.又AB是O的直径,则∠ABP=90°.又四边形ABPC的内角和等于360°,所以∠P+∠BAC+∠ACP+∠ABP=360°.所以∠P=80°.9答案:分析:要证BE·BF=BC·BD,只需证BEBCBDBF,即证明△BEC∽△BDF.由∠DBF为公共角,只需再找一组角相等,为此,过点B作O的切线,构造弦切角.证明:如图,过点B作O的切线BG,则AB⊥BG.又AD是O的切线,∴AD⊥AB,∴BG∥AD,∴∠GBC=∠BDF.又∵∠GBC=∠BEC,∴∠BEC=∠BDF.又∠CBE=∠DBF,∴△BEC∽△BDF.∴BEBCBDBF.∴BE·BF=BC·BD.10答案:分析:(1)很明显∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.证明:(1)∵BD∥MN,∴∠CDB=∠DCN.又∠BAE=∠CDB,∴∠BAE=∠DCN.又直线MN是O的切线,∴∠DCN=∠CAD.∴∠BAE=∠CAD.又∠ABE=∠ACD,AB=AC,∴△ABE≌△ACD.(2)∵∠EBC=∠BCM,∠BCM=∠BDC.∴∠EBC=∠BDC.∴CB=CD=4.∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,∴∠BEC=∠EBC+∠ABE=∠ABC.又AB=AC,∴∠ABC=∠ECB.∴∠BEC=∠ECB.∴BE=BC.5