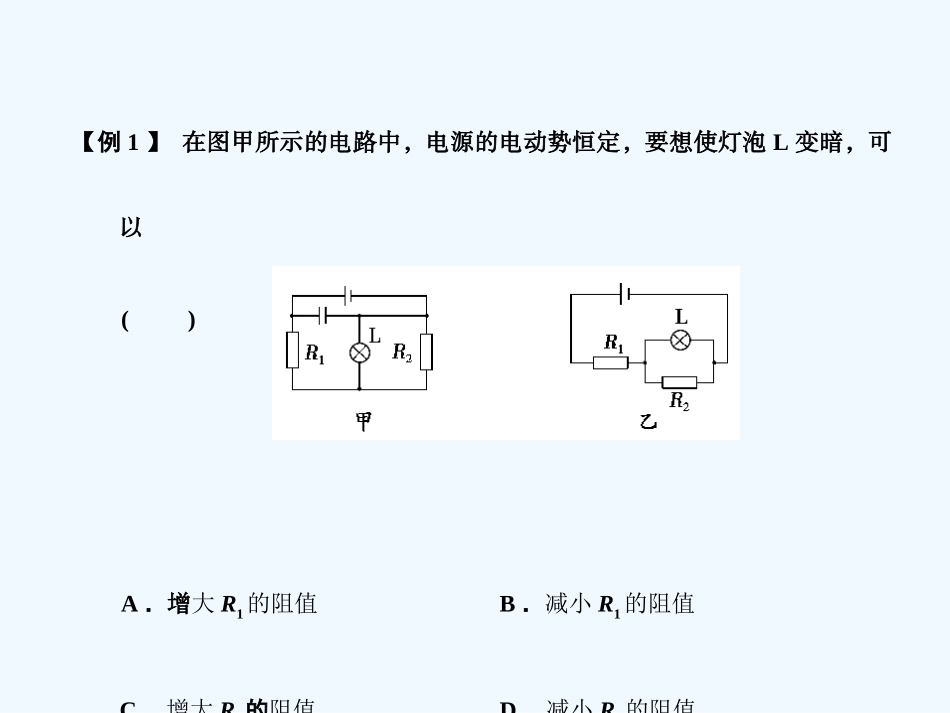
解恒定电流电路问题的常见思维方法1.极限思维法极限思维法是把某个物理量推向极端,即极大和极小或极限位置,并以此作出科学的推理分析,从而给出判断或导出一般结论.当题目要求定性地判断某一具体的物理量的变化情况或变化趋势时,可假设其他变量为极端的情况,从而就能较快地弄清该物理量的变化趋势,达到研究的目的.选择题不同于其他题型,有时对结果的得出,不需要很严密的计算,只要能够大致地了解并弄清楚其结果的范围或变化趋势就行了.因此,在做选择题时,采用极限思维法极为简便且可以大大缩短做题时间.物理思想方法与高考能力要求(十)【例1】在图甲所示的电路中,电源的电动势恒定,要想使灯泡L变暗,可以()A.增大R1的阻值B.减小R1的阻值C.增大R2的阻值D.减小R2的阻值解析:因电容器具有“隔直通交”的特征,所以其电路可等效画为图乙.当R2的阻值减少并趋于零时,L被短路,灯泡L变暗;当R1的阻值增大并趋近于无穷大时,可视为断路,总电流趋于零时,灯泡L也变暗,所以选项A、D正确.答案:AD2.等效电源法(1)讨论定值电阻消耗的功率时,一般直接利用公式P=I2R或P=进行求极值.(2)讨论可变电阻消耗的最大功率时可用等效电源法,将其他串联电路的电阻R0与电源的内阻r之和看作新的电源内阻,再利用外电阻等于内电阻时,电源输出功率最大进行分析.【例2】如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源内电阻,以下说法中正确的是()A.当R2=-R1+r时,R2上获得最大功率B.当R2=R1+r时,R1上获得最大功率C.当R2=0时,R1上获得最大功率D.当R2=0时,电源的输出功率最大解析:在讨论R2的电功率时,可将R1视为电源内阻的一部分,即将原电路等效为外电阻R2与电动势E、内阻为(R1+r)的电源(等效电源)连成的闭合电路如右图所示,R2的电功率是等效电源的输出功率,显然当R2=R1+r时,R2获得的电功率最大,选项A正确.在讨论R1的电功率时,由I=及P1=I2R1可知,R2=0时,R1获得的电功率最大;故选项B错误,选项C正确,在讨论电源的输出功率时,(R1+R2)为外电阻,内电阻r恒定,由于题目没有给出R1和r的具体数值,所以当R2=0时,电源输出功率并不一定最大,故选项D错误.答案:AC3.特殊值法【例3】如图电路中,电源相同,各电阻器阻值相等,各电流表的内阻相等且不可忽略不计.电流表读出的电流值分别为I1、I2、I3、I4.下列关系式中正确的是()A.I1=I2B.I1<I4C.I2=2I1D.I2<I3+I4解析:因电流表的内阻不可忽略,采用特殊值法,设电流表内阻与各电阻器的阻值R相等,电源内阻为零,则I3=I4=E/(2R),I2=E/(5R/3),I1=E/(5R),显然有I1<I4,I3+I4=E/R>I2,故选项B、D正确.答案:BD4.能量守恒法【例4】某商场安装了一台倾角为30°的自动扶梯,该扶梯在电压为380V的电动机带动下以0.4m·s-1的恒定速率向斜上方移动,电动机的最大输出功率为4.9kW,不载人时测得电动机中的电流为5A.若载人时扶梯的移动速度和不载人时相同,则这台自动扶梯可同时乘载的最多人数为_______.(设人的平均质量为60kg,g取10m·s-2)解析:设可同时乘载最多人数为n,此时,电动机处于最大输出功率状态,在该状态下,电动机的输出功率一方面转化为扶梯转动所需功率,另一方面转化为n个人以恒定速度向上移动所需功率.根据能量转化与守恒定律,有4900W=380×5W+mngvsin30°W,解得n=25.答案:255.转换研究对象法【例5】如图所示,电池的内阻可忽略不计,电压表和可变电阻R串联接成通路,如果R的阻值减为原来的1/3时,电压表的读数由U0增加到2U0,则下列说法正确的是()A.流过R的电流增大为原来的2倍B.R消耗的电功率增加为原来的4倍C.R两端的电压减小为原来的2/3D.若R的阻值减小到零,那么电压表的示数变为4U0解析:多数同学分析此题时选可变电阻器为研究对象,因为4个选项中都问的是有关R的问题;但R的电阻、电压、电流均非定值,判断不出各量的定量变化.若灵活地转移为分析电压表,其电阻为定值,当它的读数由U0增加到2U0时,通过它的电流一定变为原来的2倍,而R与电压表串联,故A选项正确.再利用P=UI和U=IR,R消耗的功率P′=(2I)2R/3=4P/3...