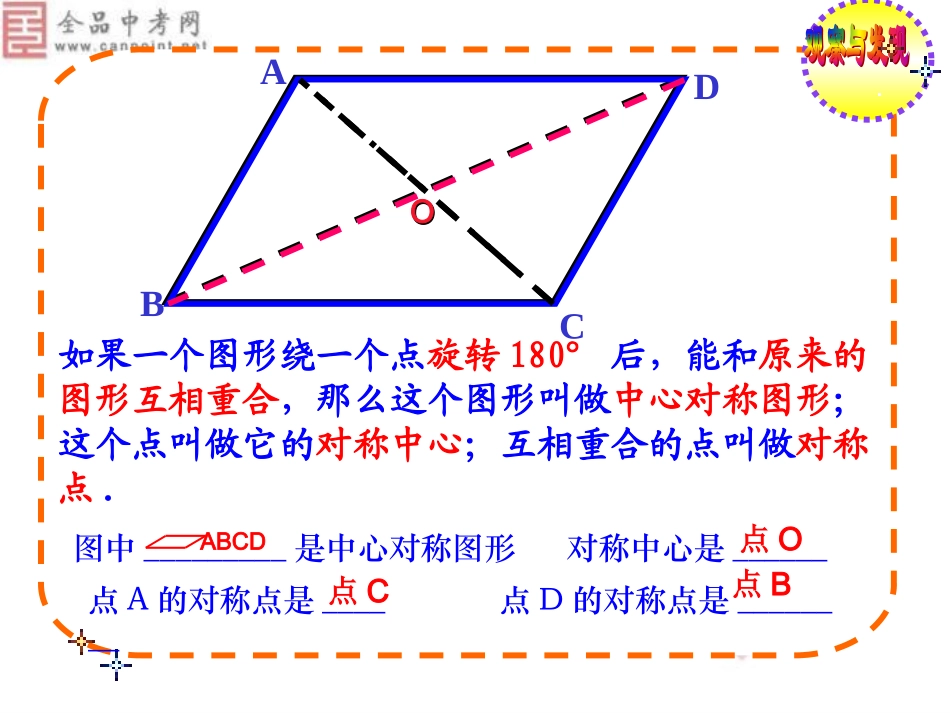
23.2.2中心对称图形(1)这些图形有什么共同的特征?都是旋转对称图形。(2)这些图形的不同点在哪?分别绕旋转中心旋转了多少度?第一个图形的旋转角度为120°或240°,第二个图形的旋转角度为72°或144°或216°或288°。后三个图形的旋转角度都为180°,第二,三个是轴对称图形。后三个图形都是旋转1800后能与自身重合OO如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.BACD图中_________是中心对称图形对称中心是______点O点A的对称点是______点D的对称点是______ABCD点C点BOO(1)平行四边形是中心对称图形吗?如果是,请找出它的对称中心,并设法验证你的结论。(2)根据上面的过程,你能验证平行四边形的哪些性质?(1)平行四边形是中心对称图形,对称中心是两条对角线的交点。(2)能验证平行四边形的对边相等、对角相等、对角线互相平分等性质。正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转900旋转1800正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?是中心对称图形旋转2700正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转3600正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?旋转nx900正方形是中心对称图形;它绕两条对角线的交点旋转900或其整数倍,都能与原来的图形重合,因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?(1)(2)(3)(4)旋转旋转图形((11))旋转旋转图形((22))旋转旋转图形((33))旋转旋转图形((44))下列图形是中心对称图形吗?点击跳转返回返回旋旋转转返回返回旋旋转转返回返回旋旋转转旋旋转转返回返回都是中心对称图形其中心就是对称中心判断下列图形是否是中心对称图形?如果是,那么对称中心在哪?选择题:(1)下列图形中即是轴对称图形又是中心对称图形的是()A角B等边三角形C线段D平行四边形C(2)下列多边形中,是中心对称图形而不是轴对称图形的是()A平行四边形B矩形C菱形D正方形A下列图形中哪些是中心对称图形?①②③④判断下列图形是不是中心对称图形:观察图形,并回答下面的问题:(1)哪些只是轴对称图形?(2)哪些只是中心对称图形?(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5)(1)(2)(3)(4)(5)(6)下面图案是中心对称图形吗?若是请指出它们的对称中心,。它是轴对称图形吗?它是中心对称图形吗?2.在①线段、②角、③等腰三角形、④等腰梯形、⑤平行四边形、⑥矩形、⑦菱形、⑧正方形和⑨圆中,是轴对称图形的有______________,是中心对称图形的有____________,既是轴对称图形又是中心对称图形的有____________.①⑤⑥⑦⑧⑨①②③④⑥⑦⑧⑨①⑥⑦⑧⑨B正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。下面的扑克牌中,哪些牌面是中心对称图形?在26个英文大写正体字母中,哪些字母是中心对称图形?ABCDEFGHIJKLMABCDEFGHIJKLMNOPQRSTUVWXYZNOPQRSTUVWXYZ1.若两个图形关于某一点成中心对称,那么下列说法:①对称点的连线必过对称中心;②这两个图形一定全等;③对应线段一定平行且相等;④将一个图形绕对称中心旋转180°必定与另一个图形重合。其中正确的是()。(A)①②(B)①③(C)①②③(D)①②③④2.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有()。(A)4(B)3(C)2(D)1CBABCDEF判断下列说法是否正确(1)轴对称图形也是中心对称图形。()...