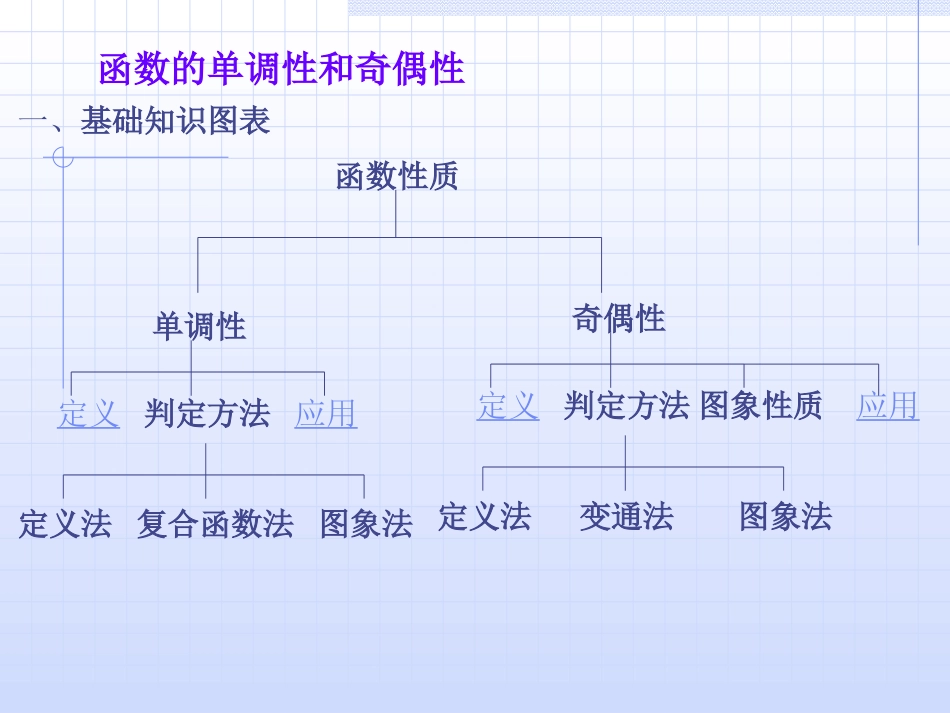
上海市复旦中学高一数学组一、基础知识图表单调性定义判定方法应用定义法复合函数法图象法奇偶性定义判定方法应用定义法变通法图象法图象性质函数性质函数的单调性和奇偶性二、函数的单调性1、如果对于属于定义域D内某个区间上的任意两个自变量的值x1,x2,当x1<x2,都有f(x1)<f(x2),那么就说f(x)在这个区间上是增函数.2、如果对于属于定义域D内某个区间上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数.3、如果函数f(x)在某个区间是增函数或减函数,那么就说f(x)在这一区间具有单调性,这一区间叫做f(x)的单调区间.函数图像能直观地显示函数的单调性.在单调区间上的增函数,它的图像是沿x轴正方向逐渐上升的;在单调区间上的减函数,它的图像是沿x轴正方向逐渐下降的.例1、画出函数y=-x2+2|x|+3的图像,并指出函数的单调区间.评析:函数单调性是对某个区间而言的,对于单独一个点没有增减变化,所以对于区间端点只要函数有意义,都可以带上.y0x-11解:函数图像如下图所示,当x≥0时,y=-x2+2x+3=-(x-1)2+4;当x<0时,y=-x2-2x+3=-(x+1)2+4.在(-∞,-1]和[0,1]上,函数是增函数.在[-1,0]和[1,+∞)上,函数是减函数.拓展:已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.评析这是涉及逆向思维的问题,即已知函数的单调性,求字母参数范围,要注意利用数形结合.解:f(x)=x2+2(a-1)x+2=[x+(a-1)]2-(a-1)2+2,此二次函数的对称轴是x=1-a.因为在区间(-∞,1-a]上f(x)是单调递减的,若使f(x)在(-∞,4]上单调递减,对称轴x=1-a必须在x=4的右侧或与其重合,即1-a≥4,a≤-3.分析要充分运用函数的单调性是以对称轴为界线这一特征.练习1、函数f(x)在(0,+∞)上是减函数求f(a2-a+1)与f()的大小关系43例2:函数f(x)是定义在(0,+∞)上的增函数,满足:f(xy)=f(x)+f(y),f(8)=3,解不等式f(x)+f(x-2)≥3[4,+∞)注:利用函数的单调性解不等式时,必须考虑条件和定义域f(a2-a+1)≤f()3422、函数、函数f(x)f(x)==4x4x22--mxmx++55在区间在区间[[--22,,+∞)+∞)上是增函数,求上是增函数,求f(1)f(1)的取值范围。的取值范围。3、设f(x)是定义域为[-1,1]上的增函数,解不等式f(x-1)g(x2),又f(x)在R上递增,而g(x1)∈R,g(x2)∈R,∴f[g(x1)]>f[g(x2)],∴f[g(x)]在[a,b]上是减函数.证明:求函数y=18+2(2-x2)-(2-x2)2的单调区间例6:例5:求函数y=f(x)在R上是减函数,求y=f(|1-x|)的单调递增区间。单调递增区间是(-∞,1]单增区间是(-∞,-1],[0,1)单减区间是(-1,0),[1,+∞)例4:2322xx求函数y=的单调区间单减区间是(-∞,-],单增区间是[2,...