（课件）《二次根式》复习VIP免费

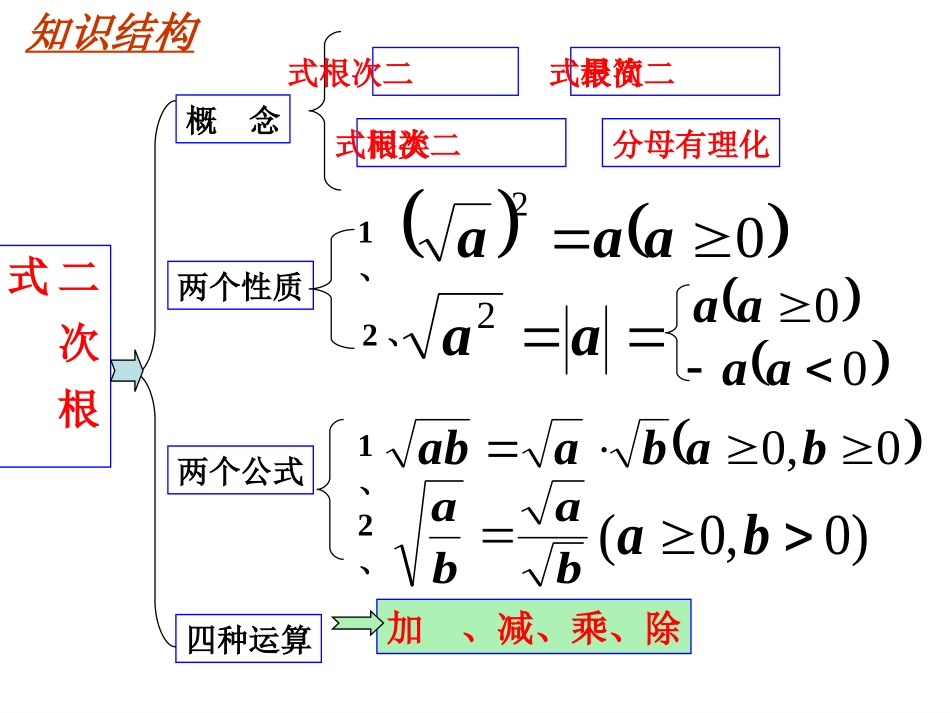
二次根式概念两个性质两个公式四种运算最简二次根式同类二次根式baba)0,0(ba0,0babaab1、2、加、减、乘、除知识结构2、1、02aaaaa20aa0aa二次根式分母有理化.的式子叫做二次根式形如a)0(a二次根式的定义:二次根式的性质:（双重非负性）.0,0aa)0(2aaaa(a≥0)-a(a≤0)==a∣∣2a1.1.下列各式中那些是二次根式？哪些不是？下列各式中那些是二次根式？哪些不是？为什么？为什么？153a100x3522ab21a144221aa⑧⑧⑦⑦⑥⑥⑤⑤④④①①②②③③２.二次根式的非负性的应用.已知：+=0,求x-y的值.yx24x已知x,y为实数,且+3(y-2)2=0,则x-y的值为()A.3B.-3C.1D.-11x解：由题意，得x-4=0且2x+y=0解得x=4,y=-8x-y=4-(-8)=4+8=12D３实数p在数轴上的位置如图所示，化简222)1(pp121)2(1ppppabab(0,0)abababa0b0（，）二次根式的乘法：算术平方根的积等于各个被开方数积的算术平方根积的算术平方根等于积中各因式的算术平方根.计算计算32453223410100033122621)()(.)()()(二次根式有除法运算的性质归纳归纳baab（a≥0，b＞0）baba（a≥0，b＞0）试一试试一试：181123(3)1050(2)232)(计算：1.被开方数不含分母2.被开方数不含开的尽方的因数或因式在二次根式的运算中，最后结果一般要求(1)分母中不含有二次根式.(2)最后结果中的二次根式要求写成最简的二次根式的形式.2.判断下列二次根式是否是最简二次根式,并说明理由。621)6())(()5(75.0)4()3()2(50)1(2222babayxbca计算a28327232531555353.解法515363332332327232aaaaaaaa2242228283解：1把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。若两个含有二次根式的代数式相乘，积不含有二次根式，则这两个代数式互为有理化因式。在进行根式计算时，利用有理化因式，有时可以化去分母中的根号，从而实现分母有理化。注意:尽管教材不要求掌握有理化因式,但是它可以为我们顺利解决相关问题提供有利的帮助.几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式.判断同类二次根式的关键是什么？(1)化成最简二次根式，(2)被开方数相同,根指数相同(都等于2)2.在下列各组根式中，是同类二次根式的是（）A.B.C.D.122,212,24ab,ab11a,a4.如果最简二次根式与是同类二次根式,求m、n的值.15mnmB12271624321253.与是同类二次根式的是()A.B.C.D.D2、二次根式加减运算的步骤:(1)把各个二次根式化成最简二次根式(2)把各个同类二次根式合并.（3）不是同类二次根式的不能合并.练习1：(1)188(2)75271(3)4863(4)23.4554C下列计算正确的是（）A.5.83211231.22BDaaa23836ＤxxxE532.2163483(2)(1220)(35)21(3)96234xxxx例计算：(1)212483316122.13123234314解：532012.2535232533xxxx1246932.3xxx232x3先化简，再合并计算22)6324).(3(638).2(26327).1(1、注意运算顺序2、运用运算律整式运算的运算律在二次根式的运算中仍然适应.26327).1(638).2(22)6324).(3(12333解：原式3633336368解：原式1848233322632224解：原式32322.22.22.2.)(12,121.12DCBAxxx则若的值。求已知：xyyxxyyx,3,19.222D33522200520067)(157)(2)(23)(23)(3)(25)(25)练习：(1)(1-5