直线与双曲线的位置关系 (2)VIP免费

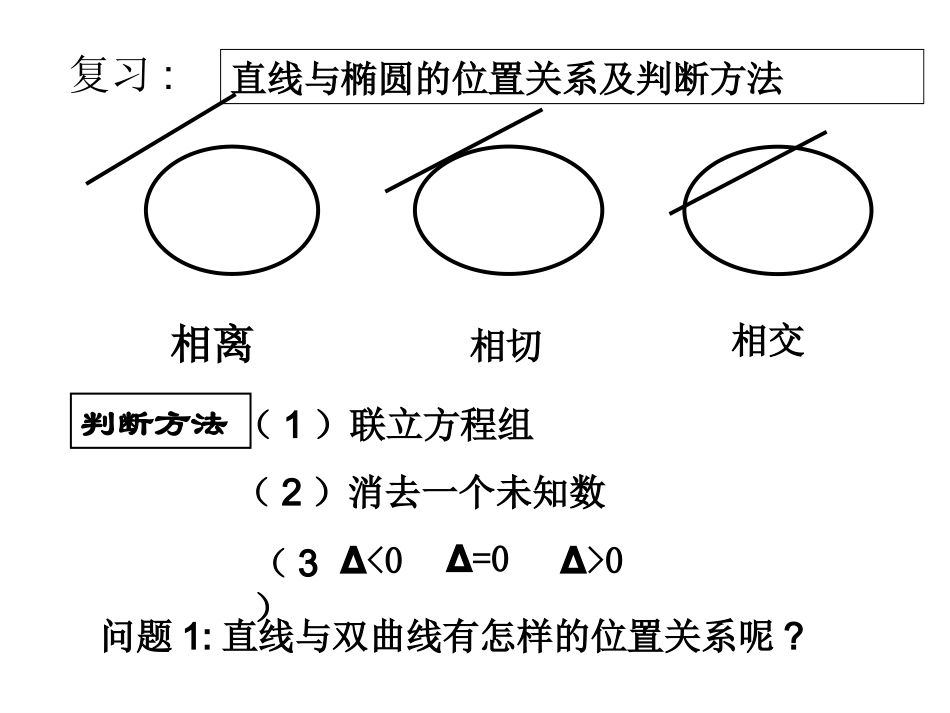
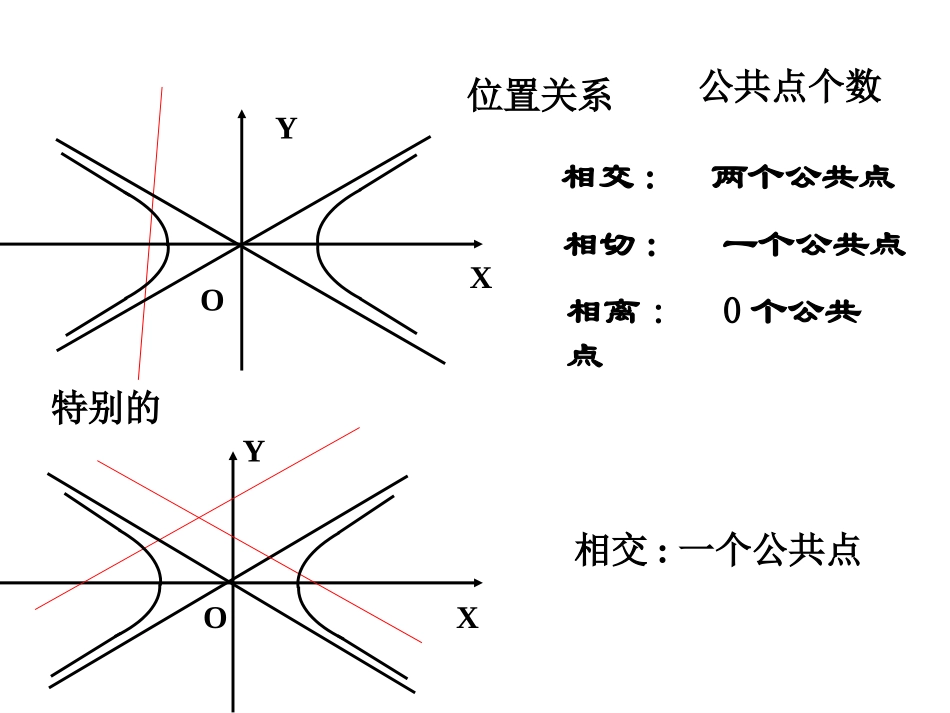
嘉祥一中高二、一科数学组嘉祥一中高二、一科数学组直线与椭圆的位置关系及判断方法判断方法（1）联立方程组（2）消去一个未知数∆<0∆=0∆>0（3）复习:相离相切相交问题1:直线与双曲线有怎样的位置关系呢?位置关系相离:0个公共点相交:两个公共点相切:一个公共点公共点个数O相交:一个公共点XY特别的YXO与椭圆一样，直线与双曲线的位置关系也是通过对直线方程与双曲线方程组成的二元二次方程组的解的情况的讨论来研究。即方程消元后得到一个一元二次方程，利用判别式⊿来讨论特别注意：直线与双曲线的位置关系中：一解不一定相切，相交不一定两解，两解不一定同支例1:如果直线y=kx－1与双曲线x2-y2=4仅有一个公共点,求k的取值范围.解:分析:只有一个公共点,即方程组仅有一组实数解.消去y整理得(1－k2)x2+2kx－5=0(1)当1－k2≠0且△=(2k)2－4(1－k2)(－5)=0时即25k方程组有一解时,(2)当1－k2=0时,即k=±1方程组有一解∴当k=±1或时,25直线与双曲线仅有一个公共点此时,直线有何特征?此时,直线有何特征?4122yxkxyk=1k=－125k25k例1.已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k的取值范围,使直线与双曲线(1)只有一个公共点;(2)有两个公共点;(3)没有公共点;(4)交于异支两点；(5)与左支交于两点.(1)k=±1，或k=±；52(4)-1＜k＜1；(3)k＜或k＞；525252(2)＜k＜；52125-k1k且例题练习:221-kx+2kx-5=022(2,0)1.PlCxyl过点的直线与双曲线：仅有一个公共点，这样的直线有条结合。解，故采用数形方程根的分布则不易求线方程，转化为此题为选择题，若设直110211300412PPPPP改变点的位置：、，；、，；、，、，BBA.1A.1B.2B.2C.3C.3D.4D.4返回返回yxxy0.0.00,.00,斜率待定的直线非渐近线与双曲线联立，消去或，得到关于或的方程。1.二次项系数等于，所得直线有什么特点？2二次项系数不等于，=0，所得直线有什么特点？3二次项系数不等于，所得直线有什么特点？4二次项系数不等于，所得直线有什么特点？想一想想一想与渐近线平行与渐近线平行与双曲线相切与双曲线相切与双曲线有两个公共点与双曲线有两个公共点与双曲线相离与双曲线相离没有公共点,△<0有一个公共点,△=0有两个公共点△>0有一个公共点,直线与渐近线平行直线与双曲线相交相切相离直线与双曲线位置关系:知识点滴例3.已知双曲线中心在原点，且一个焦点为F(，0)，直线y=x-1与其相交于M、N两点，MN的中点的横坐标为，则此双曲线的方程为（）23722.134xyA22.143xyB22.152xyC22.125xyDDD11222222222222422212222MxyNxy1.717a17y=x-17a,72a280222,2723xy1.25yyyxxaxaxaaaxxaa2222222解：设，，，x由题意，双曲线方程可设为aax由消去，得aaa所求双曲线方程为BA例4过双曲线的右焦点作倾斜角为30°的直线，交双曲线于A、B两点，求|AB|.22136xyF1oF2xy163||5AB=典型例题:双曲线中的弦长问题例5.以P（1，8）为中点作双曲线为y2-4x2=4的一条弦AB，求直线AB的方程。典型例题:解法一：（1）当过P点的直线AB和x轴垂直时，直线被双曲线截得的弦的中点不是P点。（2）当过P点的直线AB和x轴不垂直时，设其斜率为k。则直线AB的方程为y-8=k（x-1）22222y-8=kx-1由,得y-4x=4k-4x+2kk-8x+8-k-4=0112212,,,,,1AxyBxyxx设则是方程的两个不等实根.1222k-4x+2kk-8x+8-k-4=02222∴Δ=4k8-k-4k-48-k-4>021,8,ABP弦的中点是2k8-k 中点坐标公式与韦达定理,得-=13k-422由13得k=12x直线AB的方程为y-81=即直线AB的方程为x-2y+15=0典型例题:112222112222,,,,44,44AxyBxyxx解法二:设则yy111112124,yyyyxxxx1,8,ABP弦的中点是12122,16.xxyy1112168,yyxx11121,2yyABxx...