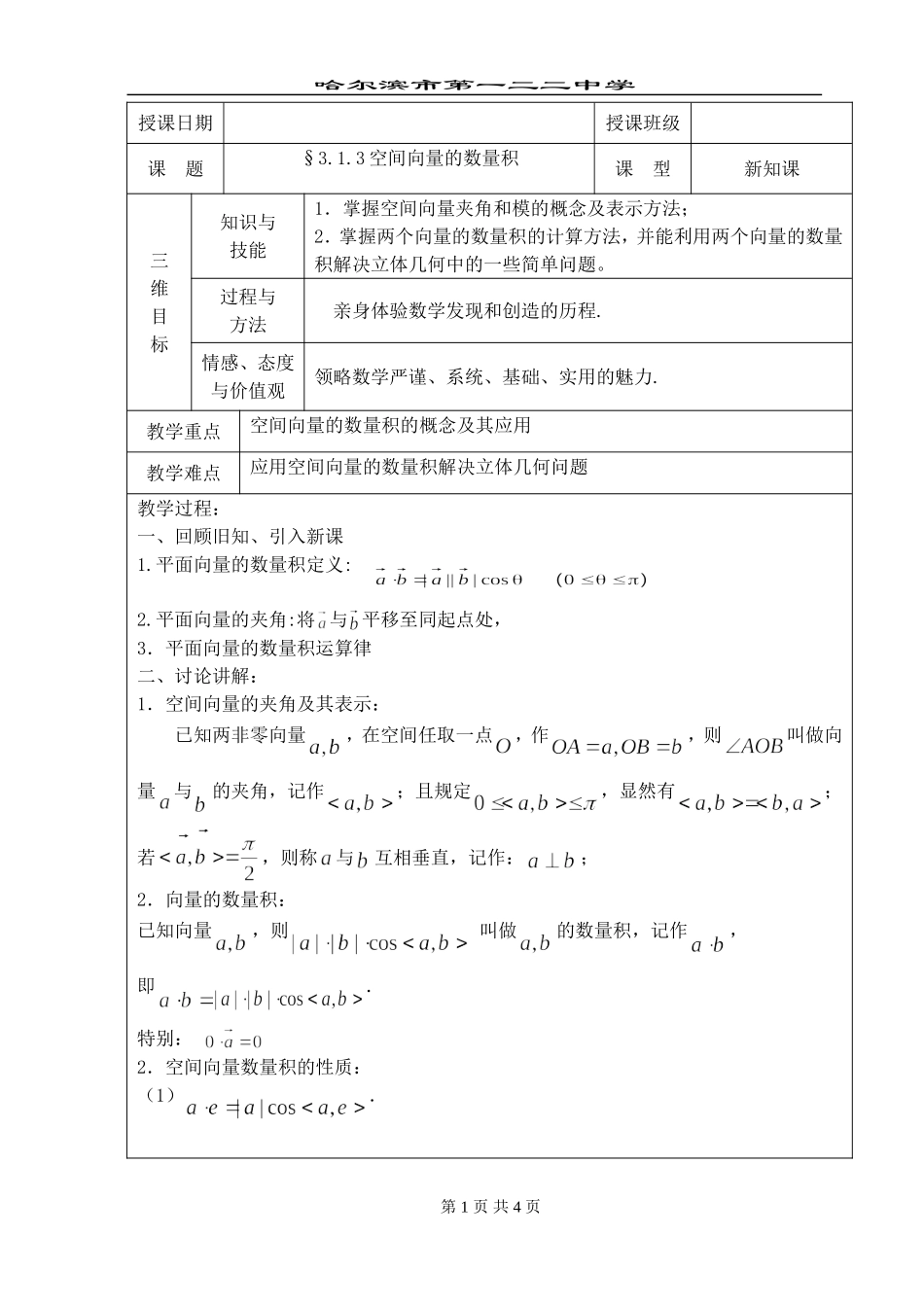
哈尔滨市第一二二中学授课日期授课班级课题§3.1.3空间向量的数量积课型新知课三维目标知识与技能1.掌握空间向量夹角和模的概念及表示方法;2.掌握两个向量的数量积的计算方法,并能利用两个向量的数量积解决立体几何中的一些简单问题。过程与方法亲身体验数学发现和创造的历程.情感、态度与价值观领略数学严谨、系统、基础、实用的魅力.教学重点空间向量的数量积的概念及其应用教学难点应用空间向量的数量积解决立体几何问题教学过程:一、回顾旧知、引入新课1.平面向量的数量积定义:2.平面向量的夹角:将与平移至同起点处,3.平面向量的数量积运算律二、讨论讲解:1.空间向量的夹角及其表示:已知两非零向量,在空间任取一点,作,则叫做向量与的夹角,记作;且规定,显然有;若,则称与互相垂直,记作:;2.向量的数量积:已知向量,则叫做的数量积,记作,即.特别:2.空间向量数量积的性质:(1).第1页共4页哈尔滨市第一二二中学(2).(3)=,叫做向量的长度或模3.空间向量数量积运算律:(1).(2)(交换律).(3)(分配律).思考:教材第90页思考题(1)判断是否成立?(2)判断是否成立?(3)判断是否成立?例1、用向量方法证明:三垂线定理及其逆定理。例2、用向量方法证明:直线和平面垂直的判定定理.三、实践反馈第2页共4页哈尔滨市第一二二中学1、正四面体的棱长为1,求(1);(2)为、的中点,求(3)(4)(5)证明:2、已知空间四边形中,,,求证:3、正四面体的棱长为1,为的中点,试求所成角的余弦第3页共4页OABC哈尔滨市第一二二中学4、如图,在空间四边形中,,,,,,,求与的夹角的余弦值.5、正方体中,分别是、、的中点,O为底面的中心,求异面直线与所成角的余弦值。6、教材第92页练习1、2、3、第4页共4页OABCAC1BCDB1MNHOD1