【创新设计】2011届高考物理一轮复习 第3章 第3课时 专题 研究动力学问题的三个基本观点课件 人教大纲版VIP专享VIP免费

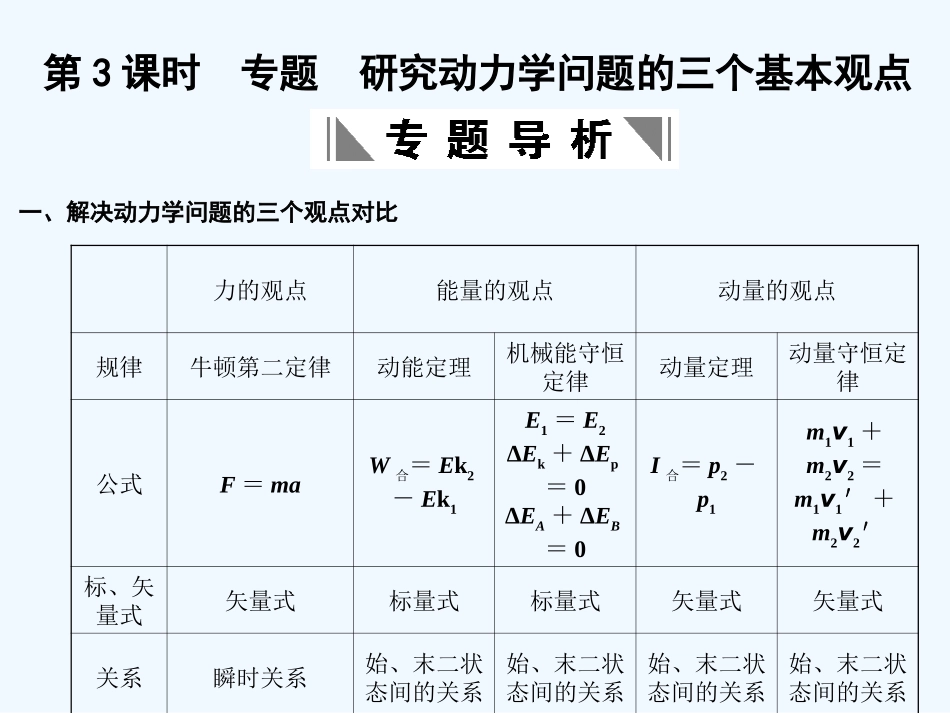
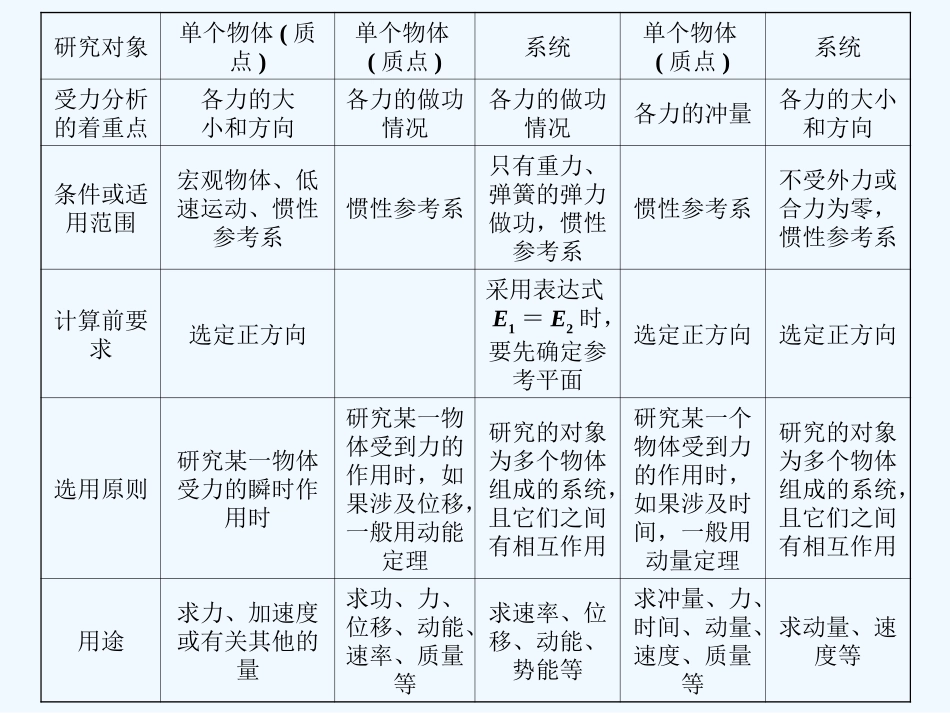
力的观点能量的观点动量的观点规律牛顿第二定律动能定理机械能守恒定律动量定理动量守恒定律公式F＝maW合＝Ek2－Ek1E1＝E2ΔEk＋ΔEp＝0ΔEA＋ΔEB＝0I合＝p2－p1m1v1＋m2v2＝m1v1′＋m2v2′标、矢量式矢量式标量式标量式矢量式矢量式关系瞬时关系始、末二状态间的关系始、末二状态间的关系始、末二状态间的关系始、末二状态间的关系一、解决动力学问题的三个观点对比第3课时专题研究动力学问题的三个基本观点研究对象单个物体(质点)单个物体(质点)系统单个物体(质点)系统受力分析的着重点各力的大小和方向各力的做功情况各力的做功情况各力的冲量各力的大小和方向条件或适用范围宏观物体、低速运动、惯性参考系惯性参考系只有重力、弹簧的弹力做功，惯性参考系惯性参考系不受外力或合力为零，惯性参考系计算前要求选定正方向采用表达式E1＝E2时，要先确定参考平面选定正方向选定正方向选用原则研究某一物体受力的瞬时作用时研究某一物体受到力的作用时，如果涉及位移，一般用动能定理研究的对象为多个物体组成的系统，且它们之间有相互作用研究某一个物体受到力的作用时，如果涉及时间，一般用动量定理研究的对象为多个物体组成的系统，且它们之间有相互作用用途求力、加速度或有关其他的量求功、力、位移、动能、速率、质量等求速率、位移、动能、势能等求冲量、力、时间、动量、速度、质量等求动量、速度等二、动量和能量综合应用常见模型模型分类特点及满足的规律弹簧处于最长(最短)状态时两物体速度相等，弹性势能最大，系统满足动量守恒、机械能守恒．m1v0＝(m1＋m2)v共，，弹簧处于原长时弹性势能为零，系统满足动量守恒、机械能守恒．m1v0＝m1v1＋m2v2，最高点：m与M具有共同水平速度，且m不可能从此处离开轨道，系统水平方向动量守恒，系统机械能守恒mv0＝(M＋m)v共，.最低点：m与M分离点．水平方向动量守恒，系统机械能守恒，mv0＝mv1＋Mv2，系统动量守恒、能量守恒：mv0＝(m＋M)v，FL相对＝(M＋m)v2.木块固定和放于光滑面上，子弹完全穿出时系统产生的热量相等三、综合应用力学三大观点解题的步骤1．认真审题，明确题目所述的物理情景，确定研究对象．2．分析所选研究对象的受力情况及运动状态和运动状态的变化过程，画出草图．对于过程复杂的问题，要正确、合理地把全过程分成若干阶段，注意分析各阶段之间的联系．3．根据各阶段状态变化的规律确定解题方法，选择合理的规律列方程，有时还要分析题目的隐含条件、临界条件、几何关系等列出辅助方程．4．代入数据(统一单位)，计算结果，必要时要对结果进行讨论．1.如图6－3－1所示，带弧形轨道的小车放在光滑的水平地面上，车左端被固定在地面上的竖直挡板挡住，已知小车的弧形轨道和水平部分在B点相切，AB段光滑，BC段粗糙，BC段长度为L＝0.75m．现有一小木块(可视为质点)从距BC面高为h＝0.2m的A点无初速度释放，恰好未从车上滑落．已知木块质量m1＝1kg，小车质量m2＝3kg，g取10m/s2.求：(1)木块滑到B点时的速度；(2)木块与BC面之间的动摩擦因数；(3)在整个过程中，小车给挡板的冲量．解析：(1)木块从A滑到B点的过程，由机械能守恒定律得：m1gh＝vB＝m/s＝2m/s.(2)m1vB＝(m1＋m2)vμm1gL＝所以μ＝＝0.2.(3)小木块与车脱离挡板前受挡板水平向右的冲量I＝m1vB－0＝m1vB＝2kg·m/s，所以小车给挡板的冲量大小为2kg·m/s，方向水平向左．答案：(1)2m/s(2)0.2(3)2kg·m/s水平向左【例1】某实验小组的同学为了搞清楚“功、能、动量”之间的关系，设计了如下实验．A．主要实验器材：一块正方体的软木块，其边长D＝16cm，质量M＝40g；一支射出速度能够连续可调的气枪，其子弹的质量m＝10g；B．主要实验过程：首先如图6－3－2所示，把正方体的软木块固定在桌面上，当子弹以20m/s的水平速度从正面射入该木块后，测得子弹能够进入木块中5cm的深度，然后，把该木块放在光滑的水平面上(例如气垫导轨上)，子弹再次从正面射入该木块，……在后者情况下，请你利用力学的知识，帮助他们分析和预测以下几个问题：(1)若子弹仍以20m/s水平速度射入木块，子弹最多能进入木块中的深度有多大？(2)若子弹仍以20m/s水平速度射入木块，在子弹射入...