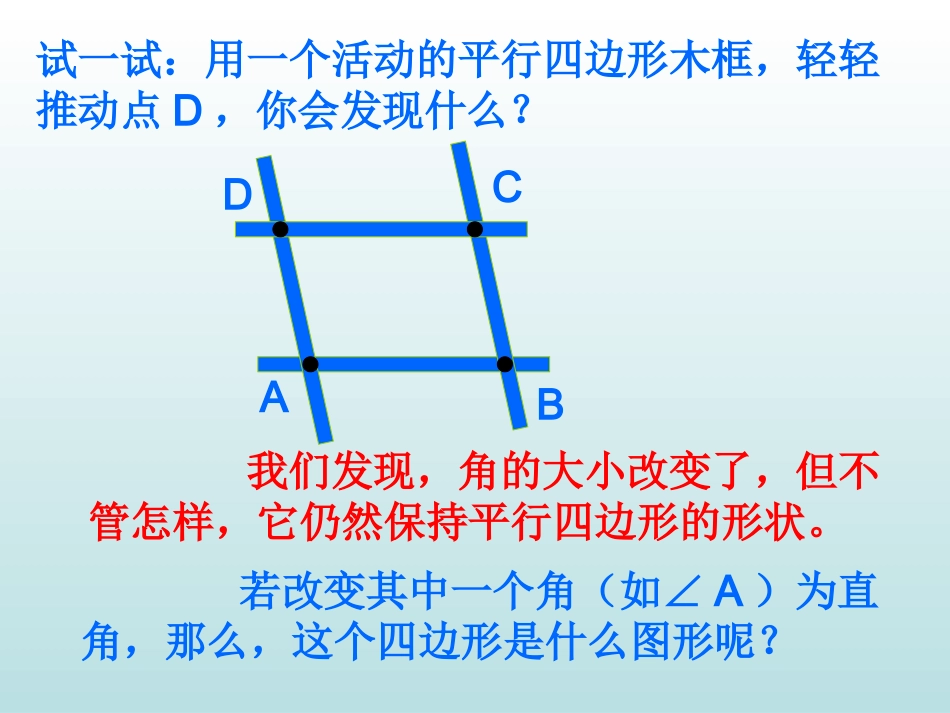
试一试:用一个活动的平行四边形木框,轻轻推动点D,你会发现什么?ABCD我们发现,角的大小改变了,但不管怎样,它仍然保持平行四边形的形状。若改变其中一个角(如∠A)为直角,那么,这个四边形是什么图形呢?ABCDABCD∠A=900矩形的定义:有一个角(如∠A=900)为直角平行四边形是矩形(或长方形)。几何表达式:在ABCD中,∠A=900∴ABCD是矩形想一想:矩形与平行四边形的关系是怎样的?矩形是特殊的平行四边形。你能说出矩形性质吗?请你说说其中的道理?小组讨论,比一比哪一个小组说得多,道理充分。(采用的方法不限)ADCBADCBO矩形的性质1、矩形是中心对称图形,它的对称中心是它两条对角线的交点。2、矩形是轴称图形,它的对称轴是经过对边中点的直线,矩形有两条对称轴。ADCBOADCB3、矩形的对边平行且相等。ADCB在矩形ABCD中ABCD∥,BCAD∥AB=CD,AD=BC4、矩形的四个角相等,每一个角都等于900。在矩形ABCD中∠A=B=C=D=90∠∠∠05、矩形的对角线相等且互相平分。ADCBO在矩形ABCD中AC=BD,OA=OC=OB=OD=AC21BD211.如图,在矩形ABCD中,找出相等的线段与相等的角。ADCBO想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三解形,有几对全等的等腰三角形?课堂练习1例1、如图,矩形ABCD的被两条对角线分成四个全等的小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少cm。ADCBO解:根据题意得:(AB+OB+OA)+(BC+OB+OC)+(CD+OC+OD)+(AD+OD+OA)=86∴(AB+BC+CD+AD)+2AC+2BD=86∵四边形ABCD是矩形∴AC=BD=13(矩形的对角线相等)∴AB+BC+CD+AD=34即矩形ABCD的周长等于34cm.例2.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴∴ACAC与与BDBD相等且互相平相等且互相平分分∴∴OA=OBOA=OB∵∠∵∠AOB=60°AOB=60°∴△∴△AOBAOB是等边三角形是等边三角形∴∴OA=AB=4(OA=AB=4(㎝㎝))∴∴矩形的对角线长矩形的对角线长AC=BD=2OA=8(AC=BD=2OA=8(㎝㎝))解:∵四边形解:∵四边形ABCDABCD是矩是矩形形DCBAo方法小结:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.1.矩形具有而一般平行四边形不具有的性质是()B.对边相等A.对角相等C.对角线相等D.对角线互相平分C课堂练习22.已知:四边形ABCD是矩形(1)若已知AB=8㎝,AD=6㎝,则AC=_______㎝OB=_______㎝(2)若已知∠DOC=120°,AC=8㎝,则AD=_____cmAB=_____cmODCBA4341053、如图,矩形ABCD的两条对角线相交于点O,且∠AOD=1200,你能说明AC=2AB吗?ADCBO解∵四边形ABCD是矩形∴OA=OB,AC=2OA∵∠AOD+AOB=180∠0∠AOD=1200∴∠AOD=600∴△AOB是等边三角形∴AB=OA∴AC=2AB课堂练习24.已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求BC的长.ABOCD解:在矩形ABCD中,OA=OB∵∠AOD=120°∴∠AOB=60°∴△AOB为等边三角形∴AB=OA=AC=4cm21在RtABC△中,224-84822AB-ACBC===cm课堂小结1、四边形、平行四边形、矩形的关系两组对边分别平行有一个角是直角对角线互相平分对角线对角线相等对边平行边对边相等对角相等角四个角都是直角2、矩形的性质(1)矩形是中心对称图形,它的对称中心是它两条对角线的交点。3、矩形的特殊性质(2)矩形是轴称图形,它的对称轴是经过对边中点的直线,矩形有两条对称轴。