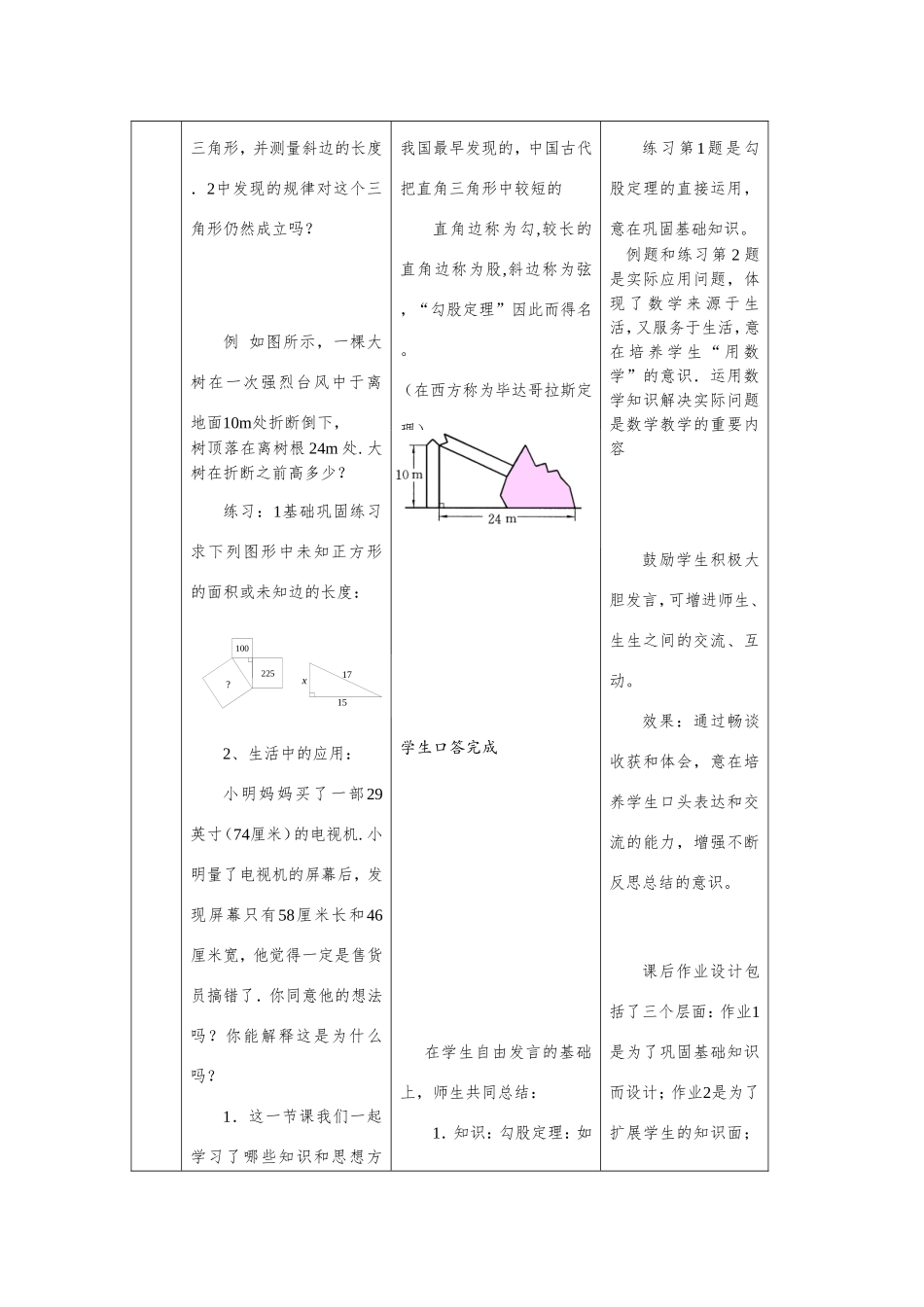
年级:初二学科:数学第二学期第1周第2课时教师:于洪杰课题:探索勾股定理2教学目标知识与能力:进一步体会数学与现实生活的紧密联系。过程与方法:体会数形结合和特殊到一般的思想方法。情感态度价值观:激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。教学重、难点重点:运用勾股定理进行简单的计算和实际运用难点:运用勾股定理进行简单的计算和实际运用学情分析勾股定理揭示了直角三角形三边之间的一种美妙关系,将形与数密切联系起来,在数学的发展和现实世界中有着广泛的作用.本节是直角三角形相关知识的延续,同时也是学生认识无理数的基础,充分体现了数学知识承前启后的紧密相关性、连续性.此外,历史上勾股定理的发现反映了人类杰出的智慧,其中蕴涵着丰富的科学与人文价值。课前准备多媒体教学过程教师活动学生活动设计意图勾股定理的简单应用(1)你能用直角三角形的边长、、来表示上图中正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?(3)分别以5厘米、12厘米为直角边作出一个直角学生尝试总结:勾股定理(gou-gutheorem):如果直角三角形两直角边长分别为、,斜边长为,那么即直角三角形两直角边的平方和等于斜边的平方。数学小史:勾股定理是1.让学生归纳表述结论,可培养学生的抽象概括能力及语言表达能力。2.通过作图培养学生的动手实践能力。弦股勾abcabc三角形,并测量斜边的长度.2中发现的规律对这个三角形仍然成立吗?例如图所示,一棵大树在一次强烈台风中于离地面10m处折断倒下,树顶落在离树根24m处.大树在折断之前高多少?练习:1基础巩固练习求下列图形中未知正方形的面积或未知边的长度:2、生活中的应用:小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?1.这一节课我们一起学习了哪些知识和思想方我国最早发现的,中国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名。(在西方称为毕达哥拉斯定理)学生独立完成学生口答完成在学生自由发言的基础上,师生共同总结:1.知识:勾股定理:如练习第1题是勾股定理的直接运用,意在巩固基础知识。例题和练习第2题是实际应用问题,体现了数学来源于生活,又服务于生活,意在培养学生“用数学”的意识.运用数学知识解决实际问题是数学教学的重要内容鼓励学生积极大胆发言,可增进师生、生生之间的交流、互动。效果:通过畅谈收获和体会,意在培养学生口头表达和交流的能力,增强不断反思总结的意识。课后作业设计包括了三个层面:作业1是为了巩固基础知识而设计;作业2是为了扩展学生的知识面;?225100x1517课堂小结布置作业法?2.对这些内容你有什么体会?请与你的同伴交流。作业:1.教科书习题17.1第1题;2.阅读《读一读》——勾股世界;3.观察下图,探究图中三角形的三边长是否满足.果直角三角形两直角边长分别为a、b,斜边长为c,那么。2.方法:①观察—探索—猜想—验证—归纳—应用;②面积法;③“割、补、拼、接”法.3.思想:①特殊—一般—特殊;②数形结合思想。作业3是为了拓广知识,进行课后探究而设计,通过此题可让学生进一步认识勾股定理的前提条件。板书设计勾股定理2一勾股定理例1如图所示,一棵大树在一次强烈台风中于离地面10m处折断倒下,树顶落在离树根24m处.大树在折断之前高多少?练习书6页练习1,作业练习书7页练习,2,3课后反思