用乘法公式分解因式VIP免费

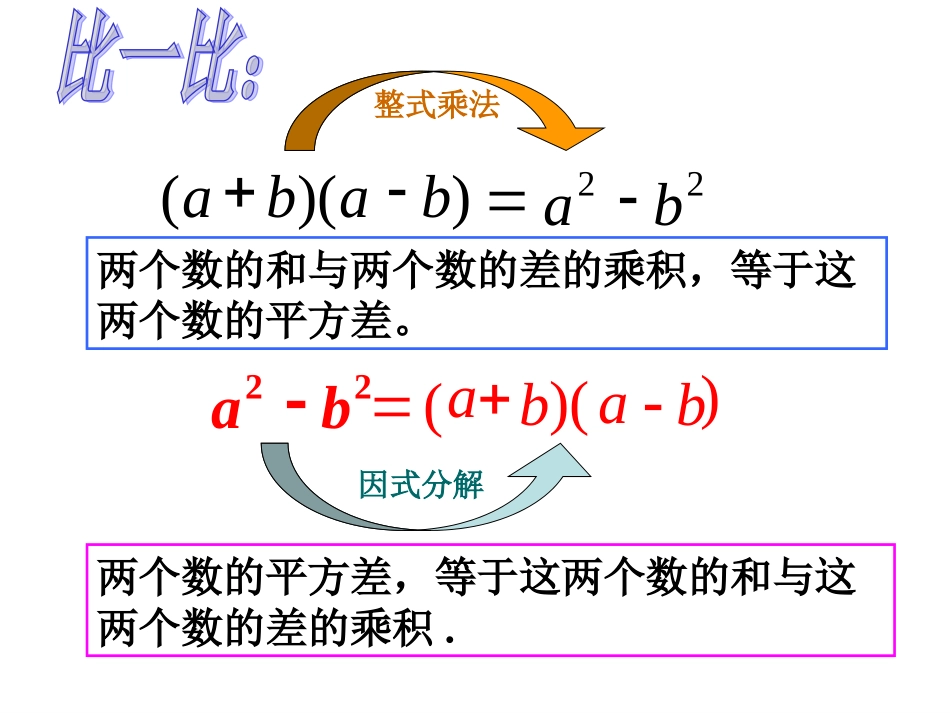
6.3用乘法公式分解因式(1)§4.3用乘法公式分解因式（1）运用平方差公式因式分解3×13.53×6.522你能不用计算器快速算出吗？=3×（13.52－6.52）=3×20×7=3×(13.5＋6.5)(13.5－6.5)))((baba22ba))((22bababa整式乘法因式分解两个数的和与两个数的差的乘积，等于这两个数的平方差。两个数的平方差，等于这两个数的和与这两个数的差的乘积.用平方差公式平方差公式分解因式))((22bababa4.3用乘法公式分解因式(1)（１）公式左边：★含有两项，这两项是异号，且负号在后面，即写成（）２－（）２的形式。(2)公式右边:★分解的结果是两个底数的和乘以两个底数的差的形式。))((22bababa▲▲▲a2-b2=(a+b)(a-b)例：16a2-1=(4a)2-12=(4a+1)(4a-1)下列多项式能否用平方差公式分解因式？说说你的理由。（1）4x2+y2(2)4x2-(-y)2(3)-4x2-y2(4)-4x2+y2(5)a2-4(6)a2+3能用平方差公式分解因式的多项式的特征：1、由两部分组成；2、两部分符号相反；3、每部分都能写成某个式子的平方。能能能不能不能不能运用a2-b2=(a+b)(a-b)例1:把下列各式分解因式：解:（1）原式=（2p)2-(mn)2=(2p+mn)(2p-mn)说明说明::公式中的公式中的aa、、bb可以是可以是单项式单项式((数字、字数字、字母母))、、还可以是还可以是多项式多项式..分解因式最后结果中如果分解因式最后结果中如果有有同类项，同类项，一定要一定要合并合并同类项。同类项。（3）原式=[(x+z)+(y+z)][(x+z)-(y+z)]=(x+y+2z)(x-y)=(x+z+y+z)(x+z-y-z)(1)-m2n2+4p2(2)x2-y2(3)(x+z)2-(y+z)2259161（2）原式=(x)2–(y)2534153534141=(x+y)(x-y)正确率+速度=效率cba222413(2)0.01s2-t2(1)16-a2(4)-1+9x2(5)(a-b)2-(c-b)2(6)-(x+y)2+(x-2y)2解:原式=(4+a)(4-a)解:原式=(0.1s+t)(0.1s-t)解:原式=(3x-1)(3x+1)解:原式=(a-c)(a+c+2b)解:原式=-3y(2x-y)ab21cab21c原式:解a2-b2=(a+b)(a-b)1.判断下列利用平方差公式分解因式是否正确,不对,请改正(3)-9+4x2=(2x-3)(2x+3)(2)-a4+b2=(a2+b)(a2-b)(5)a2-(b+c)2=(a+b+c)(a-b+c)(6)s2-t2=(-s+t)(-s-t)××(b+a2)(b-a2)(a+b+c)(a-b-c)√√(s-t)(s+t)a2-b2=(a+b)(a-b)==[-(s-t)][-(s+t)](4)-1-x2=(1-x)(1+x)(1)x2-4y2=(x+4y)(x-4y)××(x+2y)(x-2y)不能分解因式判断ma+mb=m(a+b)m是各项的公因式a2-b2=(a+b)(a-b)例2.分解因式4x3y-9xy3(2)提取公因式后,多项式还能继续分解因式吗?4x3y-9xy3=xy(4x2-9y2)4x3y-9xy3=xy(4x2-9y2)=xy(2x+3y)(2x-3y)(1)能分解因式吗?用什么方法?[注意]:1.一般地,因式分解时有公因式先提公因式2.因式分解时要分解彻底。平方差公式:a2-b2=(a+b)(a-b)把下列各式分解因式①x4-81y4②2a³-8a1.解:原式=(x²+9y²)(x²-9y²)2.解:原式=2a(a2-4)=(x²+9y²)(x+3y)(x-3y)=2a(a+2)(a-2)993-99=99(992-1)=99(99+1)(99-1)=99x100x981、请问993-99能被100整除？结论：993-99能被100整除。温馨提示：（1）能否提取公因式？（2）提取公因式后，还能继续分解因式吗？1.若n为整数，则（2n＋1)2－(2n－1)2能被8整除吗?请说明理由.2.运用本节所学的知识，把9991分解成两个整数的积.