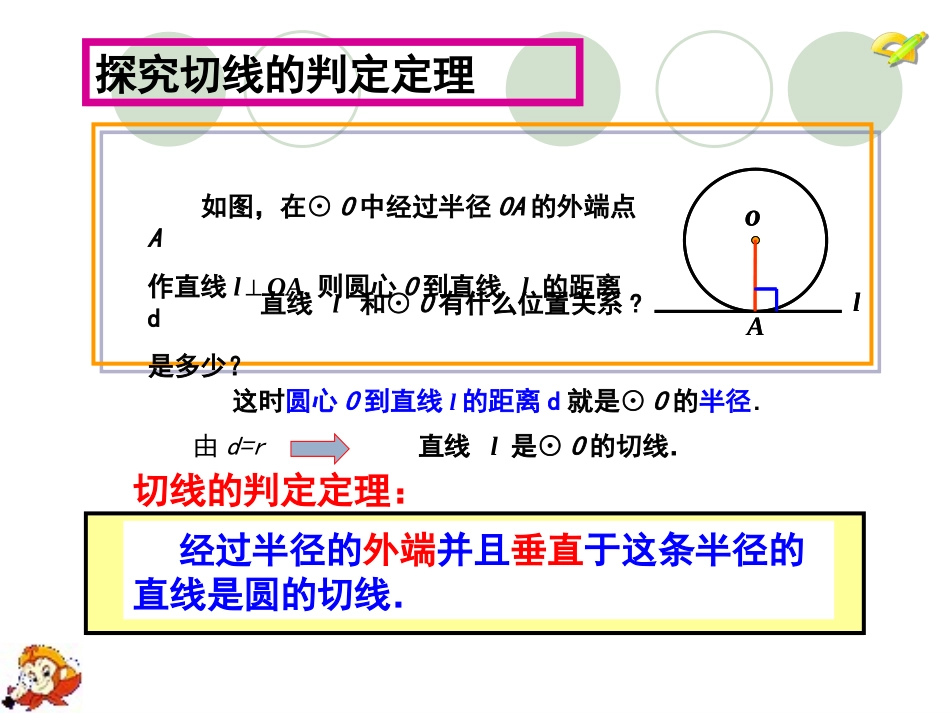
24.2直线和圆的位置关系(第2课时)杨伟华小城子九年一贯制学校新课标2011人教版九年级上册1.直线与圆有哪些位置关系?(1)定义法:由________________的个数来判断;(2)数量法:由_________________________的关系来判断。3、以上两种方法中,是如何判断直线与圆相切的呢?直线与圆的公共点圆心到直线的距离d与半径r直线与圆相交、相切、相离。2.怎样判定直线与圆的位置关系?复习直线和圆的位置关系如图,在⊙O中经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离d是多少?这时圆心O到直线l的距离d就是⊙O的半径.经过半径的外端并且垂直于这条半径的直线是圆的切线.Alo切线的判定定理:直线l和⊙O有什么位置关系?由d=r直线l是⊙O的切线.Alo探究切线的判定定理下面图中直线l与圆相切吗?为什么?lOA不相切不相切lOAOA不相切OlAOl下雨天当你快速转动雨伞时飞出的水珠,在砂轮上打磨工件飞出的火星中,存在与圆相切的现象吗?水珠和火星是沿什么方向飞出去的?下雨天当你快速转动雨伞时飞出的水,在砂轮上打磨工件飞出的火星,都是沿着圆的切线的方向飞出的.已知一个圆和圆上的一点,如何过这个点画出圆的切线?画一画:OAl将刚才思考中的问题反过来,如图,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?切线的性质定理:圆的切线垂直于过切点的半径.Al可以用反证法证明这个结论.可以用反证法证明这个结论.O探究切线的性质定理M证明:连接OC.∵OA=OB,CA=CB,∴△OAB是等腰三角形,OC是底边AB上的中线.∴OC⊥AB.∴AB是⊙O的切线.C(连半径)(证垂直)C例1:如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.OBAC运用切线的性质和判定定理解决简单问题例2:已知:△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.ABODC1.看图,你发现与例1证切线的条件有什么区别吗?2.由切线的判定定理可知,要证明切线需要什么条件?如何添加辅助线?1.看图,你发现与例1证切线的条件有什么区别吗?2.由切线的判定定理可知,要证明切线需要什么条件?如何添加辅助线?1.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线.证明:∵∠ABT=45°,AT=AB,∴∠ATB=∠ABT=45°.∴∠TAB=180°-∠ATB-∠ABT=90°.∴TA⊥OA.∴AT是⊙O的切线.·ABTO∵OA是⊙O的半径,课堂练习2.如图,AB是⊙O的直径,直线l1、l2是⊙O的切线,A、B是切点,l1、l2有怎样的关系?证明你的结论.·OABl1l2证明:l1∥l2∵l1是⊙O切线,∴l1⊥OA.∵l2是⊙O切线,∴l2⊥OB.∵AB为⊙O的直径,∴l1∥l2.3.如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,求证:AP=BP.BPOA4.如图,以O为圆心的两个同心圆中,AB、CD是大圆的弦,且AB=CD,又AB是小圆的切线,点P为切点,求证:CD是小圆的切线.BPOACDEAlo课堂小结这节课你有哪些收获?教科书习题24.2第12题.布置作业