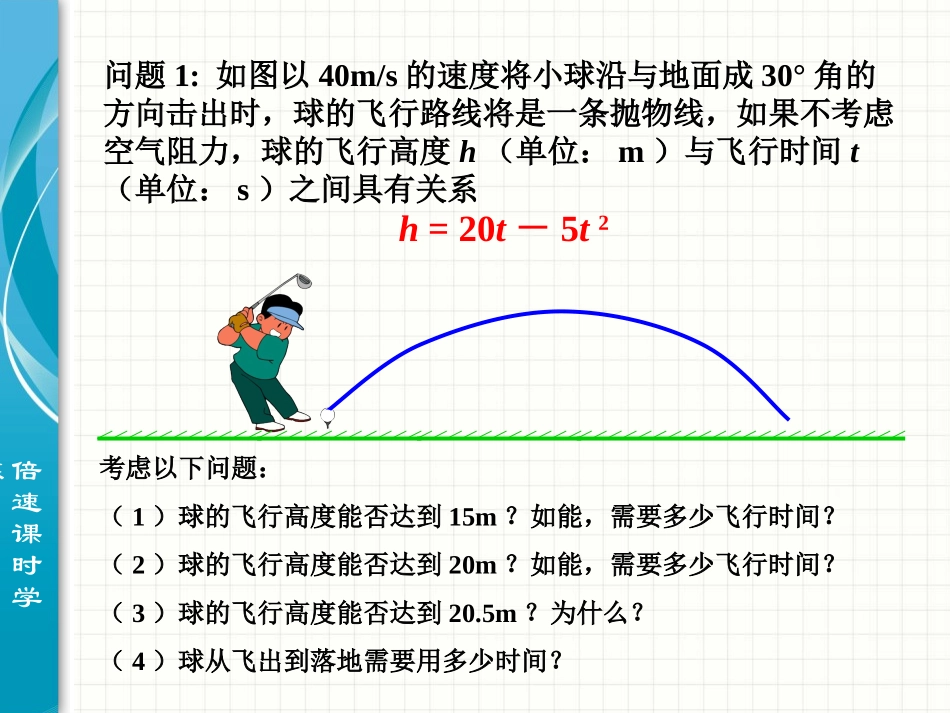
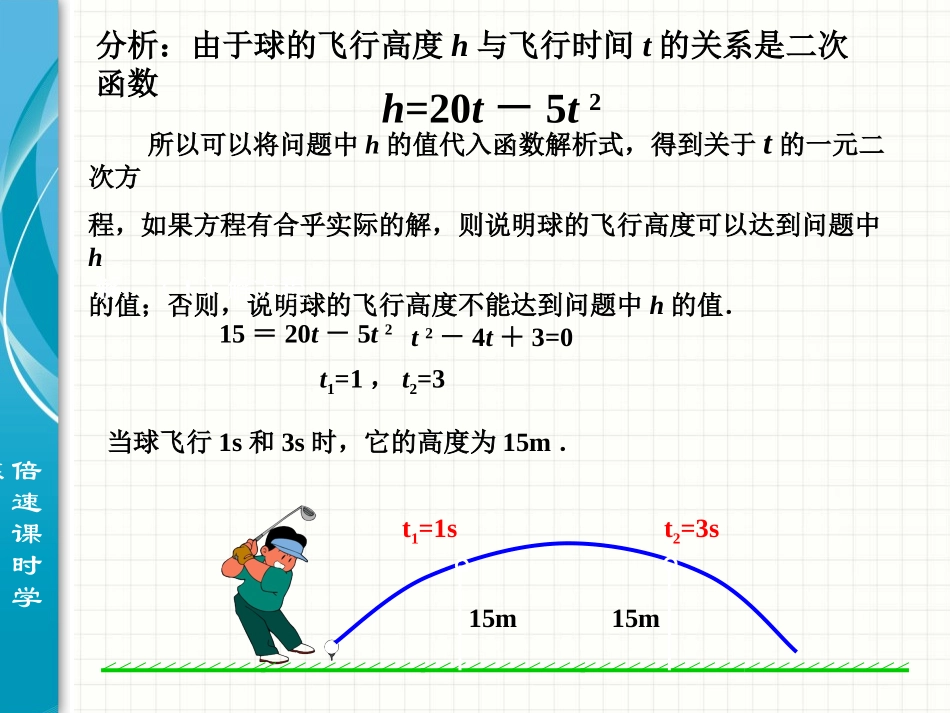
22.2二次函数与一元二次方程倍速课时学练问题1:如图以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2考虑以下问题:(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?(3)球的飞行高度能否达到20.5m?为什么?(4)球从飞出到落地需要用多少时间?倍速课时学练所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h的值;否则,说明球的飞行高度不能达到问题中h的值.解:(1)解方程15=20t-5t2t2-4t+3=0t1=1,t2=3当球飞行1s和3s时,它的高度为15m.分析:由于球的飞行高度h与飞行时间t的关系是二次函数h=20t-5t2t1=1st2=3s15m15m倍速课时学练(2)解方程20=20t-5t2t2-4t+4=0t1=t2=2当球飞行2s时,它的高度为20m.t1=2s20m(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?倍速课时学练(3)解方程20.5=20t-5t2t2-4t+4.1=0因为(-4)2-4×4.1<0,所以方程无解.球的飞行高度达不到20.5m.20m(3)球的飞行高度能否达到20.5m?为什么?倍速课时学练(4)解方程0=20t-5t2t2-4t=0t1=0,t2=4当球飞行0s和4s时,它的高度为0m,即0s时球从地面发出,4s时球落回地面.0s4s(4)球从飞出到落地需要用多少时间?倍速课时学练从上面可以看出,二次函数与一元二次方程关系密切.一般地,我们可以利用二次函数y=ax2+bx+c深入讨论一元二次方程ax2+bx+c=0例如,已知二次函数y=-x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3(即x2-4x+3=0).反过来,解方程x2-4x+3=0又可以看作已知二次函数y=x2-4x+3的值为0,求自变量x的值.倍速课时学练问题2(1)下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?y=x2-x+1y=x2+x-2y=x2-6x+9y654321-1-2-3-2-1123456xO倍速课时学练(2)当x取公共点的横坐标时,函数值是多少?y=x2-x+1y=x2+x-2y=x2-6x+9y654321-1-2-3-2-1123456xO倍速课时学练(3)由二次函数的图象,你能得出相应的一元二次方程的根吗?二次函数与一元二次方程具有怎样的联系?x2+x-2=0x2-6x+9=0x2-x+1=0y=x2-x+1y=x2+x-2y=x2-6x+9y654321-1-2-3-2-1123456xOy654321-1-2O倍速课时学练(2)二次函数的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点,这对应着一元二次方程根的三种情况:没有实数根,有两个相等的实数根,有两个不等的实数根.一般地,从二次函数y=ax2+bx+c的图象可知(1)如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数的值是0,因此x=x0就是方程ax2+bx+c=0的一个根.倍速课时学练由上面的结论,我们可以利用二次函数的图象求一元二次方程的根.由于作图或观察可能存在误差,由图象将得的根,一般是近似的.问题3(1)利用函数图象求方程x2-2x-2=0的实数根.解:作y=x2-2x-2的图象,它与x轴的公共点的横坐标大约是-0.7,2.7.所以方程x2-2x-2=0的实数根为x1≈-0.7,x2≈2.7-222464-48-2-4y=x2-2x-2(2.7,0)(-0.7,0)倍速课时学练问题(2)利用函数图象求方程x2-2x-2=—2的实数根.-222464-48-2-4y=x2-2x-2(2.7,0)(-0.7,0)(3)利用函数图象,当方程x2-2x-2=k有实数根时,k的范围。(4)利用函数图象,不等式x2-2x-2>0时,x的范围。(5)利用函数图象,不等式x2-2x-2<0时,x的范围。(6)利用函数图象,当方程︱x2-2x-2︳=k有两个不相等实数根时,k的范围。AB3.7(8)利用函数图象,直线AB:y1=kx-2,当y1>y时,求自变量x的范围。(7)利用函数图象,直线AB:y1=kx-2,当y1=y时,求自变量x的范围。倍速课时学练练习:1.汽车刹车后的距离S(单位:m)与行驶时间t(单位为:s)的函数关系式S=15t-6t2,汽车刹车后停下来行驶5米,求汽车刹车后停下来的时间是多少?解:由函数关系可得:5=15t-6t2解方程得x1≈0.98x2≈28.75(不符合实际舍去)所以汽车刹车后停下来的时间为0.98s.倍速课时学练2.一个滑雪者从85m长的山坡滑下,滑行的距离为S(单位:m)与滑行的时间t(单位:s)的函数关系式是S=1.8t+0.064t2,他通过这段山坡需要多长时间?解:由函数关系可得:85=1.8t+0.064t2解方程得t1=25t2=-53.125(不符合实际舍去)他通过这段山坡需要25秒的时间