特殊角的三角函数课件好VIP免费

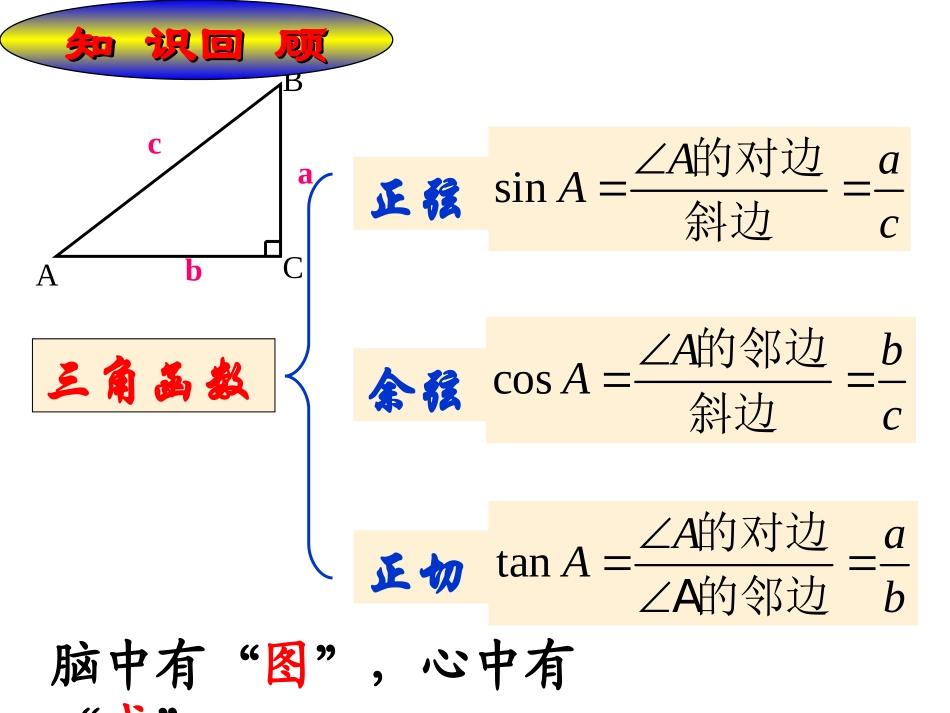
灵宝实验中学周碧洁sinAaAc的对边斜边cosAbAc的邻边斜边tanAaAb的对边A的邻边三角函数正弦余弦正切ABCabc脑中有“图”，心中有“式”知识回顾知识回顾你能求出一副三角板中各个锐角的度数吗？学习目标1、能根据正弦、余弦、正切、余切的定义，求出30°、45°、60°角的三角函数值。2、熟记30°、45°、60°角的三角函数值。3、能运用三角函数解决可以转化为直角三角形问题的简单的实际问题。特殊角三角函数值两块三角尺中有几个不同的锐角？分别求出这几个锐角的正弦值、余弦值和正切值．CAB∠BCA=90°，∠A=30°可以知道,AB=2BC还可以求出AC=BC3212sin30sinBCBCABBCA2323cos30cosBCBCABACA333tan30tanBCBCACBCA那么,此时,sin60°、cos60°、tan60°你可以求出来吗?假如∠A=45°，你能求出sin45°、cos45°、tan45°吗？CAB显然，△ABC是一个等腰直角三角形，有AC=BC∠BCA=90°，∠A=45°进而AB=AC2222sin45sinBCBCABBCA222cos45cosBCBCABACA1tan45tanBCBCACBCA30°45°60°sinαcosαtanα2122222132323133角α三角函数认真观察一下特殊角三角函数值表格,你能发现什么规律？观察特殊角的三角函数表，发现规律：(1)当0°＜α＜90°时,α的正弦值，正切值随着角度的增大而增大，随着角度的减小而减小;α的余弦值随着角度的增大而减小，随着角度的减小而增大;(2)互余两角的锐角三角函数值之间的关系sin60°=cos30°Sin45°=cos45°Sin30°=cos60°tan30°tan60°=130°45°60°sinαcosαtanα2122222132323133角α三角函数1.1.已知角，求值已知角，求值求下列各式的值求下列各式的值2sin30°+3tan30°+tan45°=2+d=2+d32.cos245°+tan60°cos30°=2=21.1.1.已知角，求值已知角，求值求锐角求锐角AA的值的值2.2.已知值，求角已知值，求角1.已知tanA=，求锐角A.32.已知2cosA-=0,求锐角A的度数.3∠A=60°∠A=60°∠A=30°∠A=30°1.1.已知角，求值已知角，求值确定值的范围确定值的范围2.2.已知值，求角已知值，求角1.在RtABC△中∠C=90°，当锐角A>45°时，sinA的值（）(A)0＜sinA＜(B)＜sinA＜1(C)0＜sinA＜(D)＜sinA＜13.3.确定值的范确定值的范围围23222223B(A)0＜cosA＜(B)＜cosA＜1(C)0＜cosA＜(D)＜cosA＜1212123232.当锐角A>30°时，cosA的值（）C1.1.已知角，求值已知角，求值确定角的范围确定角的范围2.2.已知值，求角已知值，求角3.3.确定值的范围确定值的范围(A)0°＜∠A＜30°(B)30°＜∠A＜90°(C)0°＜∠A＜60°(D)60°＜∠A＜901.当∠A为锐角，且tanA的值大于时，∠A（）33B4.4.确定角的范围确定角的范围1.1.已知角，求已知角，求值值2.2.已知值，求角已知值，求角3.3.确定值的范围确定值的范围4.4.确定角的范确定角的范围围确定角的确定角的范围范围2.当∠A为锐角，且sinA=那么∠A（）(A)0°＜∠A＜30°(B)30°＜∠A＜45°(C)45°＜∠A≤60°(D)60°＜∠A≤90°A1/5例例33、、(1)(1)如图，在如图，在RtABC△RtABC△中，∠中，∠C=90°C=90°，，AB=,BC=AB=,BC=。求∠。求∠AA的度数。的度数。(2)(2)如图如图,,已知圆锥的高已知圆锥的高AOAO等于圆锥的底面等于圆锥的底面半径半径OBOB的倍的倍,,求求α.α.63363CAB(1)OBA(2)例1：如图，AC是△ABD的高，BC=15cm，∠BAC=30°，∠DAC=45°，求AD.ACBD如图，在△ABC中，已知BC=1+，∠B=60°，∠C=45°，求AB的长.3ACBD101(32)4cos30|12|3°020091(1).2sin603tan30(1)3°°(2).请你谈谈对本节学习内容的体会和感受。今天你有什么收获?67页课后练习1,2