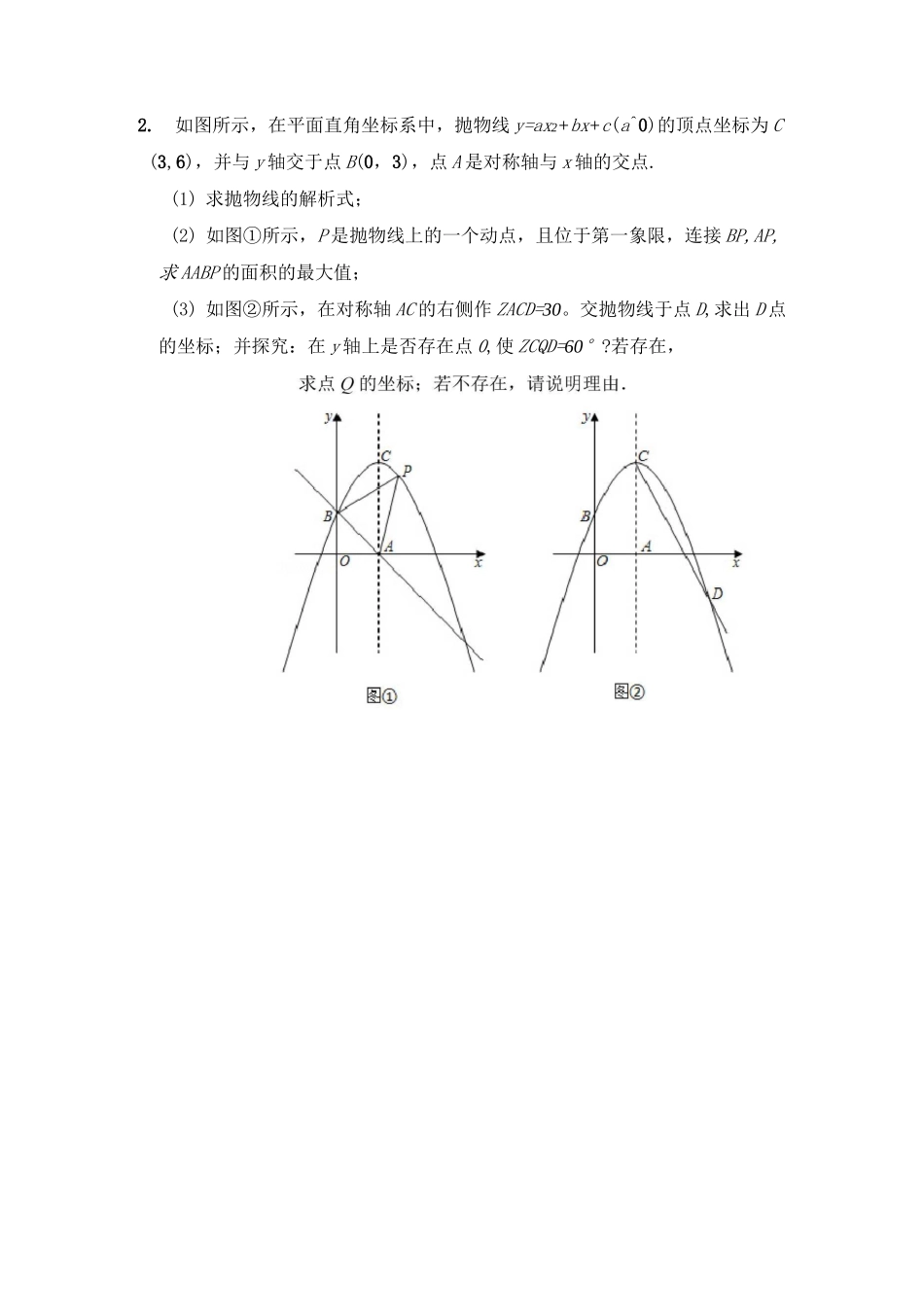
中考复习二次函数抛物线综合大题1..如图1,已知抛物线y=ax2+bx+3(aHO)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点户,使厶CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)在(1)中抛物线的对称轴上是否存在点0,使得AOAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形2.如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c(a^0)的顶点坐标为C(3,6),并与y轴交于点B(0,3),点A是对称轴与x轴的交点.(1)求抛物线的解析式;(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接BP,AP,求AABP的面积的最大值;(3)如图②所示,在对称轴AC的右侧作ZACD=30。交抛物线于点D,求出D点的坐标;并探究:在y轴上是否存在点0,使ZCQD=60°?若存在,3.已知,如图,抛物线y=ax2+bx+c(aHO)的顶点为M(1,9),经过抛物线上的两点A(-3,-7)和B(3,眈)的直线交抛物线的对称轴于点C.(1)求抛物线的解析式和直线AB的解析式.(2)在抛物线上A、M两点之间的部分(不包含A、M两点),是否存在点D,使得SADAC=2S^DCM?若存在,求出点D的坐标;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点A,M,P,Q为顶点的四边形是平行四边形时,直接写出满足条件的点P的坐标备用4.如图,抛物线y=ax2+bx-2(aHO)与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,直线y=-x与该抛物线交于E,F两点.(1)求抛物线的解析式.(2)P是直线EF下方抛物线上的一个动点,作PH丄EF于点H,求PH的最大值.(3)以点C为圆心,1为半径作圆,OC上是否存在点M,使得ABCM是以CM为直角边的直角三角形?若存在,直接写出M点坐标;若不存在,说明5•如图,抛物线y=ax2+bx-5与坐标轴交于A(-1,0),B(5,0),C(0,-5)三点,顶点为D.(1)请直接写出抛物线的解析式及顶点D的坐标;(2)连接BC与抛物线的对称轴交于点点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF//DE交抛物线于点F,设点P的横坐标为m.①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.②过点F作丄BC于点求APFH周长的最大值.6•在直角坐标平面内,直线y=gx+2分别与x轴、y轴交于点A、C.抛物线y囂2+^x+c经过点A与点C,且与x轴的另一个交点为点B点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;(2)联结BC、BD,且BD交AC于点如果AABE的面积与AABC的面积之比为4:5,求ZDBA的余切值;(3)过点D作DF丄AC,垂足为点F,联结CD.若ACFD与△AOC相似,7.如图,二次函数y=ax2+bx+c(aHO)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).(1)求二次函数的解析式和直线BD的解析式;(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)在抛物线上是否存在异于B、D的点0,使ABDO中BD边上的高为2•込?若存在求出点Q的坐标;若不存在请说明理由.8•已知抛物线y=ax2+bx+3经过点A(1,0)和点B(-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.(1)________________________抛物线的解析式为,抛物线的顶点坐标为;(2)如图1,连接OP交BC于点D,当S小:SABPD=1:2时,请求出点D的坐标;(3)如图2,点E的坐标为(0,-1),点G为x轴负半轴上的一点,ZOGE=15°,连接PE,若ZPEG=2ZOGE,请求出点P的坐标;(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.9•如图,抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y+2经过点A,C.(1)求抛物线的解析式;(2)点P在抛物线在第一象限内的图象上,过点P作x轴的垂线,垂足为D,交直线AC于点连接PC,设点P的横坐标为m.①当APCE是等腰三角形时,求m的值;②过点C作直线PD的垂线,垂足为尸.点F关于直线PC的对称点为F,当点F落在坐标轴上时,请直接写出点P的坐标.10.如图,抛物线y=ax2+bx+c经过点A(-2,5),与x轴相交于B1,0),C(3,0)两点.(1)求抛物线的函数表达式;(2)点D在抛物线的对称轴上,且位于...