华师大版八年级上册142勾股定理的应用VIP免费

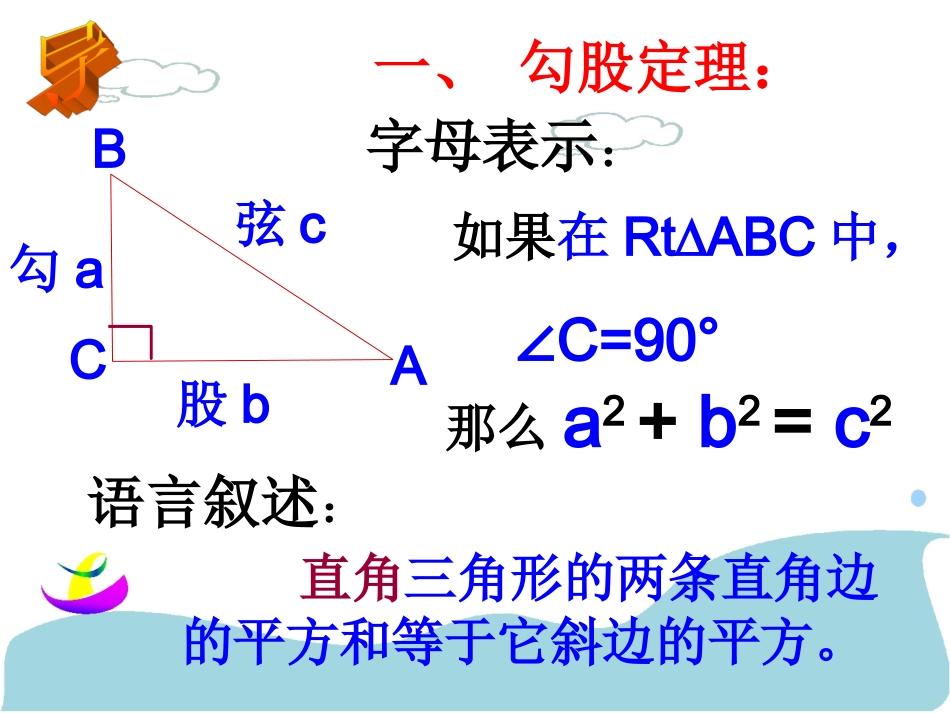
14.2勾股定理的应用1华东师大版数学八年级（上）ABC勾a股b弦c一、勾股定理：直角三角形的两条直角边的平方和等于它斜边的平方。那么a2+b2=c2如果在Rt∆ABC中，∠C=90°语言叙述：字母表示：如果三角形的三边长a、b、c满足那么这个三角形是直角三角形。222cba二、直角三角形的判定（勾股定理的逆定理）1、一圆柱体的底面周长为２4cm,高AB为5cm,BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C,试求出爬行的最短路程．ABDCACBD解在RtACD△中，AD=12，CD=5由勾股定理得AC2=AD2+CD2=122+52=169∴AC=13ABCDo最短路程问题1、一只蚂蚁从点A出发，沿着底面周长为48，高为14的圆柱的侧面爬行到CD的中点o，试求出爬行的最短路程。ABDC4O247解如图，在Rt△ＡDO中，AD＝24，OD=7∴AO2＝AD2+DO2＝576+49＝625AO＝25（勾股定理）答：最短路程约为25。ABCDo2472、如图，边长为1的正方体中，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是（）.（A）3（B）√5（C）2（D）1AB分析：由于蚂蚁是沿正方体的外表面爬行的，故需把正方体展开成平面图形（如图）.CABC21如图，在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁，现要向顶点B处爬行，已知蚂蚁爬行的速度是1厘米/秒，且速度保持不变，问蚂蚁能否在20秒内从A爬到B？B蛋糕ABAB最短路程问题挑战“试一试”挑战“试一试”::一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图的某工厂，问这辆卡车能否通过该工厂的厂门?说明理由。ABCD2米2.3米例ABMNOC┏DH2米2.3米解：CD＝22ODOC228.01CH＝0.6＋2.3＝2.9(m)＞2.5(m).答：高度上有0.4m的余量，卡车能通过厂门．＝＝0.6m，OC＝1m(大门宽度一半)，OD＝0.8m（卡车宽度一半）在RtOCD△中，由勾股定理得１、立体图形中路线最短的问题，往往是把立体图形展开，得到平面图形．根据“两点之间，线段最短”确定行走路线，根据勾股定理计算出最短距离．２、在解决实际问题时，首先要画出适当的示意图，将实际问题抽象为数学问题，并构建直角三角形模型，再运用勾股定理解决实际问题．应用勾股定理解决实际问题的一般思路：1、已知：等边△ABC的边长是6cm(1)求高AD的长.(2)求SABC.△ABDC∟例解：（1）∵△ABC是等边三角形，AD是高，在Rt△ABD中，AB=6，BD=3，根据勾股定理，∵AD2=AB2-BD2cmBDABAD2793622∴（三线合一）321BCBDABDC∟例(2)SABC△＝ADBC21=(cm2)393321=×6×1．等腰△ABC的腰长为10cm，底边长为16cm，则底边上的高为＿＿＿＿，面积为__________．2．等腰直角△ABC中，∠C=90°，AC=3cm，BC=4cm.那么它的斜边上的高为＿＿＿．6cm248cm16cm10cmDABC3cmABC4cmD2.4cm甲船以每小时30海里的速度，从A处向正北方向航行，同时乙船从A处以每小时40海里的速度向正西方向航行，两小时后，甲、乙两艘轮船相距多少海里？ABC甲乙304022××=60=80(海里)(海里)甲船以每小时30海里的速度，从A处向正北方向航行，同时乙船从A处以每小时40海里的速度向正西方向航行，两小时后，甲、乙两艘轮船相距多少海里？ABC解：如图，在Rt∆ABC中，BC2=AB2+AC2BC=(30×2)2+(40×2)2=100(海里)答：甲乙两船相距100海里。甲船在港口A正南方向60海里的B处向港口行进，同时，在甲船正东方向80海里的C处有乙船也向港口行进,甲船的速度为30海里/时,乙船的速度为40海里/时.··ABC问:1.甲、乙两船谁先到达港口?2.先到的船比后到的船提前几小时?6080２.把几何体适当展开成平面图形，再利用“两点之间线段最短”性质来解决最短路程问题。１.要记住勾股定理及逆定理的内容。