实数复习课-(2)VIP免费

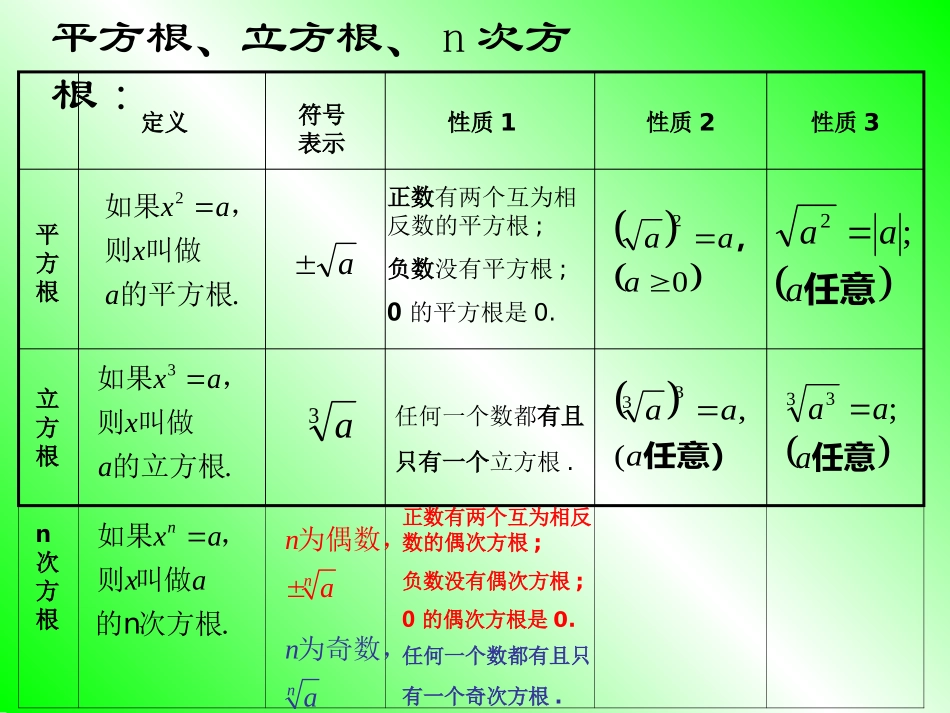
平方根立方根符号表示3aa定义性质1正数有两个互为相反数的平方根;负数没有平方根;0的平方根是0.任何一个数都有且只有一个立方根.02aaa，任意）aaa(,33性质2性质3任意aaa;2任意aaa;33平方根、立方根、n次方根:.2的平方根叫做则，如果axax.3的立方根叫做则，如果axaxn次方根.nxaxa如果，则叫做的n次方根nna为偶数，nna为奇数，正数有两个互为相反数的偶次方根;负数没有偶次方根;0的偶次方根是0.任何一个数都有且只有一个奇次方根.•实数的绝对值及其几何意义aa(a>0)0(a=o)-a(a<0)=实数的有关定义：•绝对值相等、符号相反的两个数叫做互为相反数；0的相反数是0.a的相反数表示为-a.•每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点也都可以用唯一的一个实数来表示..无理数的概念：.实数的分类:有理数无理数零负有理数正无理数负无理数正有理数实数实数的有关定义：无限不循环小数叫做无理数练习：2（１）的平方根是_______;（２）若x2=2,则x=_______;（３)36的算术平方根是_______;（４)32的五次方根是_______;（５)16的四次方根是______.169432621、填空:(6)2的平方根是____；49(8)平方根是______；27781_______.的平方根是32、选择题：(1)下面说法中正确的是（）．A无理数包括正无理数、零和负无理数．B无理数是用根号形式表示的数．C无理数是开方开不尽的数，D无理数是无限不循环小数．(2)若-b是a的平方根，那么（）Ab2=a2Ba=b2Cb=-a2Da=-b2(3)下列说法中，正确的是（）A0的平方根是0B1的平方根是1C-1的平方根是-1D（-1）2的平方根是-13、判断题:()164()255()()()0()()(8)1aa３１、1-９是无理数。4２、等于或-。5３、互为相反数的两个数的立方根也互为相反数。４、当ａ０时，一定是无理数。５、只有的立方根是本身。６、８３２３＝４３。７、－一定是负数。、的平方根与立方根相同。•实数的大小比较：近似数与有效数字：近似数的精确度表示方法：精确到哪一位保留几个有效数字对于一个近以数，从左边第一个不等于零的数字起，往右到末位数字为止的所有数字都叫做这个数的有效数字。2例用四舍五入法，把下列各数按括号内的要求取近似值；（1）0.00234(精确到万分位)（2）-5.0078(精确到百分位)（3）3.14159(精确到0.001)（4）83420(精确到万位)（5）83420(精确到千位)利用科学记数法练习136例用四舍五入法，把下列各数按括号内的要求取近似值：(1)1.05048(保留五个有效数字)(2)-1.05048(保留四个有效数字)(3)0.05048(保留三个有效数字)(4)5048(保留两个有效数字)(5)1.0510(保留四个有效数字)练习230.0199920042000.练习、判断题1近似数99.0的精确度与近似数99一样.2近似数99.0的精确度与近似数99的有效数字个数一样.3近似数8千万和近似数8000万的精确度一样.4保留两个有效数字的近似值是0.020.5精确到百位的近似值是•实数的大小比较：•分数指数幂及其运算mna=nma(m,n是正整数)0.1anmna=?实数的运算：5723；<>(2=4)•实数的运算性质：02aaa，任意aaa;20,0,.abaaababbb设1计算：2计算：15132-81１－１２４１２１２3４９32216533215;21032103;235621515;42;352112;63233.0abc6abca-b+c-a-c+b、、、三个数在数轴上的点如图所示，求：