2.1.1直线的斜率VIP免费

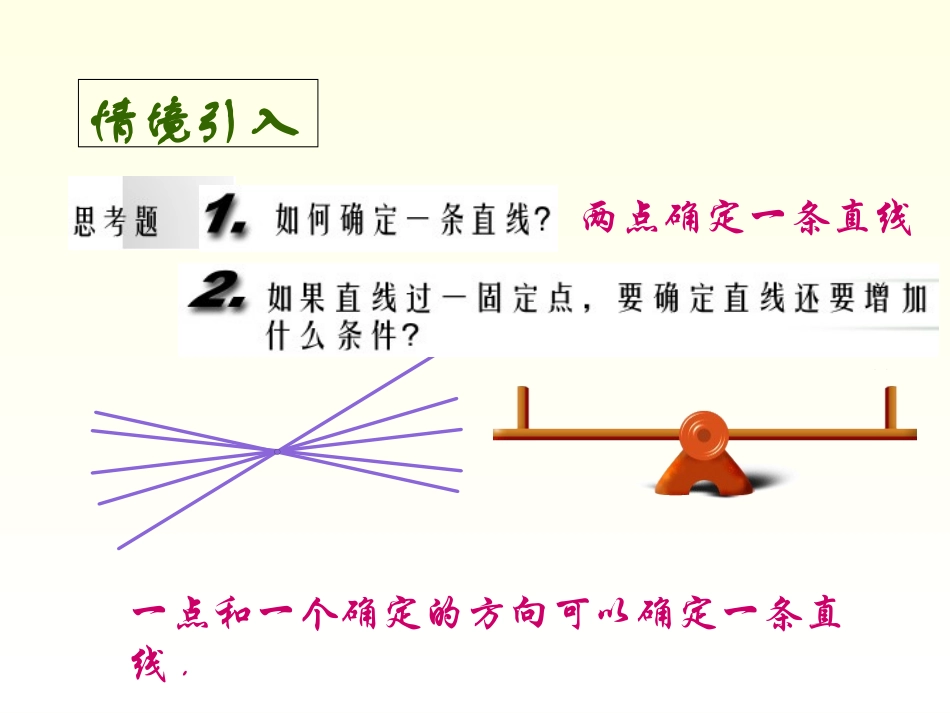
如果代数与几何各自分开发展,那么它的进步将十分缓慢,而且应用范围也很有限.但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进.____拉格朗日问题情境情境引入一点和一个确定的方向可以确定一条直线.两点确定一条直线为什么大桥的引桥要很长?思考:在平面直角坐标中，如何刻画直线的倾斜程度？为什么滑滑梯要很高才刺激?结论：坡度越大，楼梯越陡．0.8m1m0.4m1m观察两个楼梯的倾斜程度坡度＝级高级宽xyOP(x1,y1)Q(x2,y2)级宽高级y2-y1x2-x1x2-x1y2-y12121yyxx实验探究1、在平面直角坐标系中，如何刻画直线的倾斜程度呢？xyo是一个定值2.对于一条与x轴不垂直的定直线的值与P、Q两点的位置有关吗?2121yyxx2121yyxxPQP’Q’MM’实验探究Q’M实验探究直线的斜率OyxP(x1,y1)Q(x2,y2)k＝y2－y1x2－x1y2－y1x2－x1已知两点P(x1,y1),Q(x2,y2),如果x1≠x2，那么直线PQ的斜率为:数学建构•例1如图，直线都经过点又分别经过点，，，试计算直线的斜率(3,2)P123,,lll123,,lll123,,lll(2,1)A(4,2)B(3,2)C135k24k30kxyABCl1l3l2数学应用直线的方向与斜率之间有何对应关系？k>0xyO（1）.k<0xyO（2）.k=0xyO（3）.直线从左下方向右上方倾斜直线与x轴平行或重合PPPPk不存在直线从左上方向右下方倾斜xyo（4）例2.经过点A(3,2)画直线，使直线的斜率分别为①;②45-A(3,2）xyoA(3,2）xy(3,2)Bxyxyo231132A(3,2）xy(3,2)Bxy(7,5)B(2,6)BC(8,-2)34数学应用12312345672.判断下列三点是否在同一直线上(1)A(0,2),B(2,5),C(3,7)(2)A(-1,4),B(2,1),C(-2,5)数学应用1.在坐标系内分别作出经过下列两点的直线，并求出直线斜率.①A（2,3）,B（4,5）②P（-2,3）,Q（2,1）1.一个概念—直线的斜率；2.两个问题—（1）已知直线上两点如何求斜率；（2）已知一点和斜率如何画出直线。3.数形结合的思想方法回顾反思本节课我们学习了什么？•P80:1,3,4课后作业