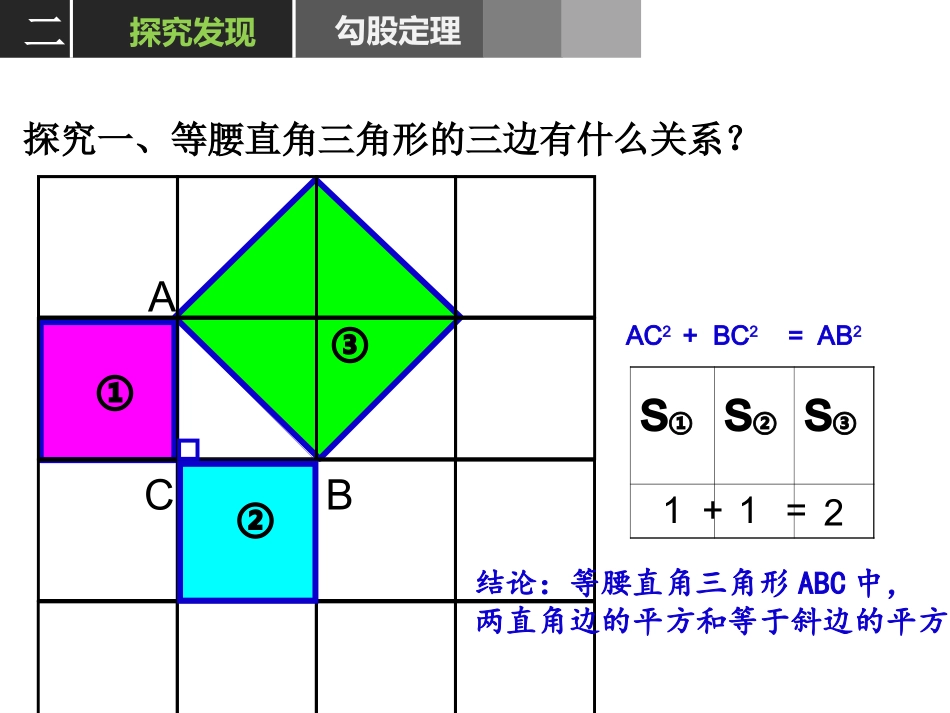
勾股定理勾股定理合肥特殊教育中心徐丽莉CBA2002年世界数学家大会会标一情景导入勾股定理①②③探究一、等腰直角三角形的三边有什么关系?ACBAC2+BC2=AB2二探究发现勾股定理s①s②s③结论:等腰直角三角形ABC中,两直角边的平方和等于斜边的平方112+=s①s②s③①②③acb探究二:一般直角三角形的三边有什么关系?a2+b2=c2猜想:任意直角三角形中,两条直角边的平方和等于斜边的平方。92516+=三定理证明勾股定理如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这四个直角三角形拼成一个大的正方形,来说明:bcbacbacbac222cba=+acabcabcabcab大正方形的面积可以表示为;也可以表示为c2abab214)(2cabcabcabcab (a+b)2=a2+2ab+b2=2ab+c2∴a2+b2=c2大正方形的面积可以表示为_____;也可以表示为_______(a+b)224abC224abC2勾股定理(毕达哥拉斯定理)如果直角三角形两直角边分别为a,b,斜边为c,那么即直角三角形两直角边的平方和等于斜边的平方.222cbaacb股勾弦两千多年前,古希腊有个哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾股世界勾股世界公元前6世纪,古希腊有个毕达哥拉斯学派,他们最先证明了勾股定理。因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。勾股定理是数学史乃至人类史上一个著名的定理。它一直以来吸引着数学家、普通学者、一般百姓,甚至美国总统的兴趣。人们目前共发现了它的367种证法,勾股定理可能是人类史上,证明方法最多的一个定理。美国第二十任总统伽菲尔德总统巧证勾股定理12S梯形=(a+b)(a+b)=(a2+b2)+ab12S梯形=c2+2·ab=c2+ab121212即:在RtABC△中,∠C=90°c2=a2+b2例1、求出下列直角三角形中未知边的长度∟x12四定理应用勾股定理例2.在Rt△ABC中,∠C=90°,a=40,c=41,求b。∟∟1234x练习1、求出下列直角三角形中未知边的长度2、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?8mBCA6m6建模勾股定理勾股定理的应用实际问题的数学建模五课堂小结勾股定理六布置作业勾股定理1、在台风“麦莎”的袭击中,一棵大树在离地面9米处断裂,树的顶部落在离树根底部12米处。这棵树折断之前有多高?2、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?(选做)勾股定勾股定理教学阐释理教学阐释CBA1、教材的地位和作用勾股定理是在学习了二次根式后学习的,是直角三角形的一条重要性质,是几何中最重要的定理之一。它揭示了直角三角形三边之间的数量关系,将数与形密切地联系起来,它有着丰富的历史背景,在理论上占有重要的地位,在数学发展史上有着非常重要的作用。学好本节不仅为下节勾股定理的逆定理打下良好基础,而且为今后学习解直角三角形奠定基础,在实际生活中用途很大。2、教学目标知识与技能:了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理;培养在实际生活中发现问题总结规律的意识和能力.过程与方法:通过创设情境,导入新课,引导学生探索勾股定理,并应用它解决问题,运用了观察、演示、实验、操作等方法学习新知。情感态度价值观:感受数学文化,激发学生学习的热情,体验合作学习成功的喜悦,渗透数形结合的思想。3、教学重难点基于以上分析我认为本节课的教学重点为:探索勾股定理并证明勾股定理,能初步应用;教学难点:理解用面积理论验证勾股定理.一教材分析勾股定理学生已经知道直角三角形两个锐角互余,也了解命题与证明,并且已经学习了二次根式的运算,能够进行一般的推理和论证,但如何通过拼图来证明勾股定理,学生对这种解决问题的途径还比较陌生,存在一定的难度,因此,我采用直观教具、多媒体等手段,让学生动手、动口、动脑,化难为易,深入浅出,让学生感...