第六章-实数的复习VIP免费

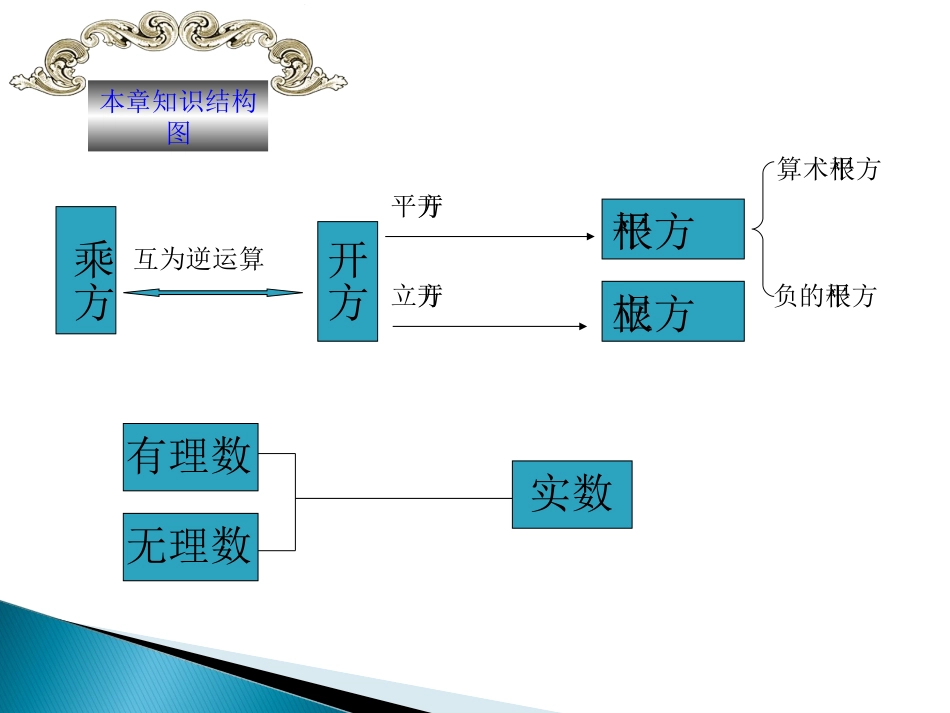
学习目标1、理解算术平方根、平方根、立方根、无理数、实数的概念（重点）2、明确实数的分类，理解实数与数轴上的点的对应关系；（重点）3、会求平方根、立方根，绝对值，相反数，会进行简单的实数运算。（难点）本章知识结构图乘方开方开平方开立方平方根立方根有理数无理数实数互为逆运算算术平方根负的平方根基本概念基本概念（1）平方根与算术平方根的概念（1）平方根与算术平方根的概念一个数的平方等于a，那么这个数叫做a的平方根（二次方根）一个数的平方等于a，那么这个数叫做a的平方根（二次方根）基本概念基本概念的平方等于a，，那么叫做a的平方根（二次方根）的平方等于a，，那么叫做a的平方根（二次方根）xxxx即X2=a，即X2=a，（2）平方根与算术平方根的性质（2）平方根与算术平方根的性质¶Á×÷£ºÕý£¬¸º¸ùºÅa£­a±íʾaµÄËãÊõƽ·½¸ùµÄÏà·´Êý基本概念基本概念的平方等于a，，那么叫做a的平方根（二次方根）的平方等于a，，那么叫做a的平方根（二次方根）xxxx即X2=a，即X2=a，（2）平方根与算术平方根的性质（2）平方根与算术平方根的性质平方根的性质：正数有2个平方根，它们互为相反数；0的平方根是0；负数没有平方根。00记作：基本概念基本概念的平方等于a，，那么叫做a的平方根（二次方根）的平方等于a，，那么叫做a的平方根（二次方根）xxxx即X2=a，即X2=a，（2）平方根与算术平方根的性质（2）平方根与算术平方根的性质（3）什么叫做开平方运算？（3）什么叫做开平方运算？求一个数的平方根的运算基本概念基本概念（2）立方根的概念（2）立方根的概念一个数的立方等于a，那么这个数叫做a的立方根一个数的立方等于a，那么这个数叫做a的立方根（2）立方根的表示与性质（2）立方根的表示与性质3a立方根的性质：一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零。基本概念基本概念（2）立方根的概念（2）立方根的概念一个数的立方等于a，那么这个数叫做a的立方根一个数的立方等于a，那么这个数叫做a的立方根（2）立方根的表示与性质（2）立方根的表示与性质3a（3）什么叫做开立方运算？（3）什么叫做开立方运算？求一个数的立方根的运算区别你知道算术平方根、平方根、立方根联系和区别吗？z.x.x.k算术平方根平方根立方根表示方法a的取值性质a3aa≥0a是任何数开方a≥0a正数0负数正数（一个）0没有互为相反数（两个）0没有正数（一个）0负数（一个）求一个数的平方根的运算叫开平方求一个数的立方根的运算叫开立方≠是本身0,100,1,-10a实数有理数无理数分数整数正整数­­0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况有关的数及一些与、)1(开不尽方的数”“”“23，、循环节的无限小数无规律或有规律但无).3(【小试牛刀】考点一：平方根与立方考点一：平方根与立方根根2、327的绝对值是（）A．3B．3C．13D．134、38=_____，38=______，64=，25121=.BBAAAA-2-2-2-28832【牛刀小试】考点二：实数及实数的大小比考点二：实数及实数的大小比较较1、写出两个你喜欢的负无理数______________(答案不唯一).3、比较大小：5______6，154，2223,2222<<<<<<2、38的相反数是______，2的倒数是______.,41把下列各数分别填入相应的集合内：把下列各数分别填入相应的集合内：把下列各数分别填入相应的集合内：把下列各数分别填入相应的集合内：,23,7,,25,2,320,5,83,94,03737737773.0（相邻两个3之间的7的个数逐次加1）有理数集合有理数集合有理数集合有理数集合无理数集合无理数集合无理数集合无理数集合,83,41,25,94,0,23,7,,2,320,53737737773.0考点三：考点三：实数分类实数分类2a2a33a33a=a0a00aa)0(aaaaa0a为任何数a为任何数a几个基本公式：（注意字母的取值范围）3a=­­­-3a为任何数a考点四、实数的运算3232等于它的相反数是正数等于本身32是负数2332）（原式23322332...