2.3.1椭圆的参数方程VIP免费

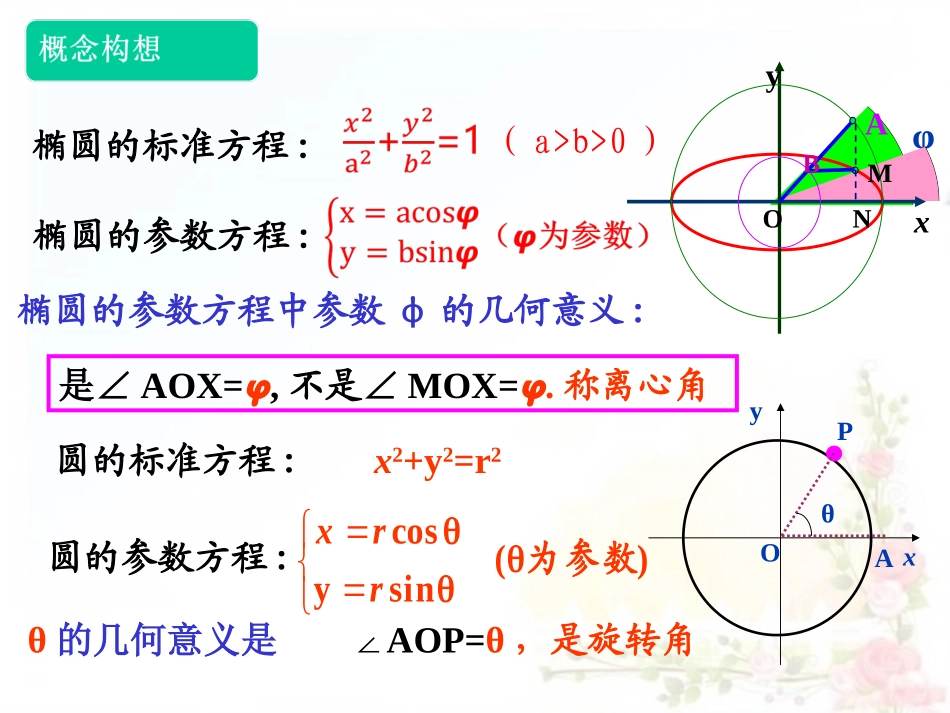
第二讲参数方程第二讲参数方程1.1.椭圆的参数方程椭圆的参数方程二.圆锥曲线的参数方程OAMxyNB解：设M(x,y)，A:(acosφ,asinφ),B:(bcosφ,bsinφ),由此:即为点M轨迹的参数方程.消去参数得:,bya12222x即为点M轨迹的普通方程.如下图，以原点O为圆心，分别以a，b（a＞b＞0）为半径作两个同心圆，设A为大圆上的任意一点，连接OA,与小圆交于点B，过点A作ANox⊥，垂足为N，过点B作BMAN⊥，垂足为M，求当半径OA绕点O旋转时点M的轨迹参数方程.演示∠XOA=φ,则（x，y）（x，y）（x，y）φOAMxyNB椭圆的标准方程:椭圆的参数方程中参数φ的几何意义:xyO圆的标准方程:圆的参数方程:x2+y2=r2)(sinycos为参数rrxθ的几何意义是∠AOP=θ，是旋转角PAθ椭圆的参数方程:是∠AOX=𝞿,不是∠MOX=𝞿.称离心角（a>b>0）练习：已知椭圆的参数方程为(是参数)，则此椭圆的长轴长为（），短轴长为（），焦点坐标是（），离心率是（）。2cossinxy4232(,0)3探究：椭圆规是用来画椭圆的一种器械，在一个十字形的金属板上有两条互相垂直的导槽，在直尺上有两个固定的滑块AB,它们可分别在纵槽和横槽中滑动，在直尺上的点M处用套管装上铅笔，使直尺转动一周就画出一个椭圆，你能说明它的构造原理吗？演示xyOP分析1平移直线l至首次与椭圆相切，切点即为所求.22204936xymxy000,M(,)消元，利用，求出进而求得切点mxyM设(3cos,2sin)是椭圆上任一点.|3cos4sin-10|5d则分析234|5cossin-10|555（）0|5cos-10|5（）00034cos,sin55其中满足05d当=0时,取最小值，0098coscos,2sin2sin55此时3398M(,)2100555Mxy时，点与直线的距离取最小值。练习动点P(x,y)在曲线上变化，求2x+3y的最大值和最小值14922yx.,2626最小值最大值3cos,2sin设xy236cos6sinxy62sin()4小结（1）椭圆的参数方程（a>b>0）注意：椭圆参数与圆的参数方程中参数的几何意义不同。（2）利用椭圆参数方程解决椭圆上的点到直线距离问题（为参数𝞿）（为参数𝞿）