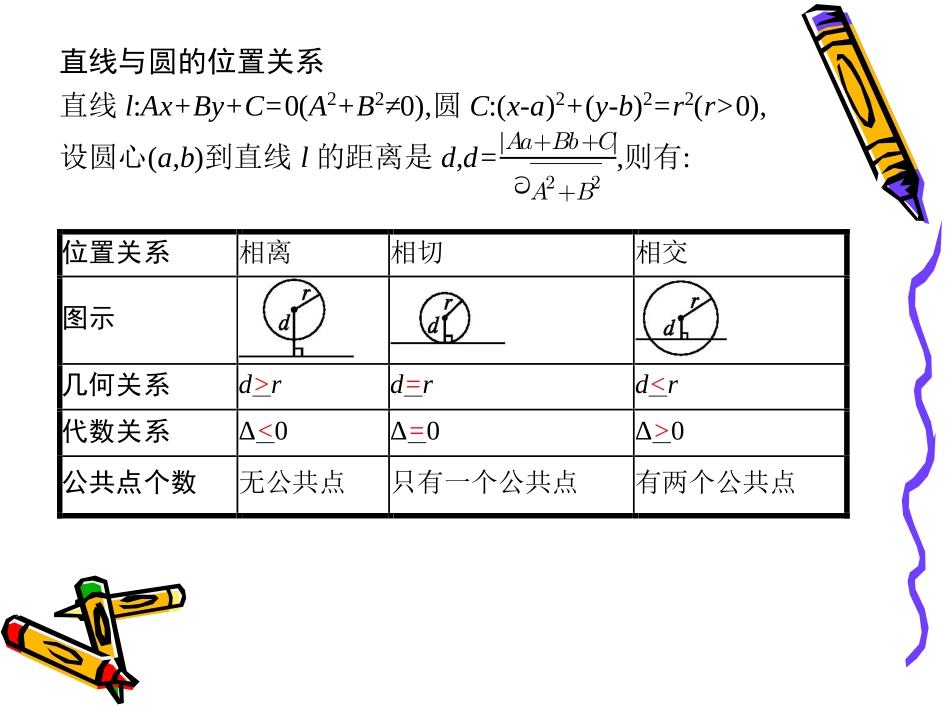
直线与圆的位置关系直线与圆的位置关系直线与圆的位置关系直线与圆的位置关系授课教师徐燕玲授课教师徐燕玲20182018年年11月月99日日直线与圆的位置关系直线l:Ax+By+C=0(A2+B2≠0),圆C:(x-a)2+(y-b)2=r2(r>0),设圆心(a,b)到直线l的距离是d,d=|𝐴𝑎+𝐵𝑏+𝐶|ට𝐴2+𝐵2,则有:位置关系相离相切相交图示几何关系d>rd=rd0公共点个数无公共点只有一个公共点有两个公共点•一.直线与圆相交•(一)判断位置关系•(二)勾股定理算弦长•(三)过一定点的弦的问题(知弦长求直线方程,最短弦)练习1.(2015年1卷新课标文)已知过点)1,0(A且斜率为k的直线l与圆1)3()2(:22yxC交于NM,两点.则k的取值范围为练习1.(2015年1卷新课标文)已知过点)1,0(A且斜率为k的直线l与圆1)3()2(:22yxC交于NM,两点.则k的取值范围为解:圆心)3,2(C到直线l:1kxy的距离11|22|2kkd得03832kk374374k例2.(2013安徽文)直线x+2y-5+5=0被圆x2+y2-2x-4y=0截得的弦长为()A.1B.2C.4D.46例2.(2013安徽文)直线x+2y-5+5=0被圆x2+y2-2x-4y=0截得的弦长为()A.1B.2C.4D.46解:圆5)2()1(:22yxC,圆心)2,1(C到直线l的距离121522d2||2122drAB,得弦长为4练习2.(2014浙江文)圆02222ayxyx截直线02yx所得弦的长度为4,则实数a的值是()A.-2B.-4C.-6D.-8练习2.(2014浙江文)圆02222ayxyx截直线02yx所得弦的长度为4,则实数a的值是()A.-2B.-4C.-6D.-8解:圆的标准方程为ayxC2)1()1(:22记圆心C到直线的距离为d,ard22222又因为211|211|22d,所以4a例3.过点)4,4(M的直线被圆0204222yxyx截得的弦长8||AB,求直线l的方程练习3.过点)3,2(M的直线l交圆9)4(22yx于BA,两点,且52||AB,求直线l的方程例4.圆0126422yxyx内一点)2,4(M,以M为中点的弦所在的直线方程为过点M的最短弦长为练习4.(2011重庆)在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.52B.102C.152D.202例5.已知直线0xya与圆心为C的圆222440xyxy相交于,AB两点,且,ACBC则实数a的值为.练习5.已知mR,直线mymmxl4)1(:2和圆C:2284160xyxy.直线l能否将圆C分割成弧长的比值为12的两段圆弧?为什么?