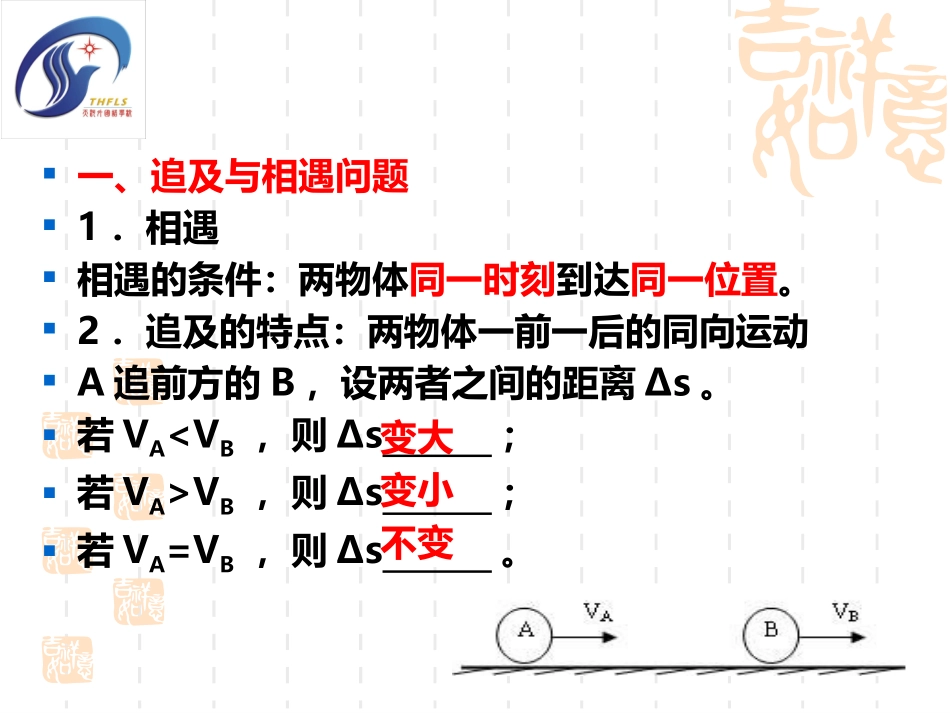
执教人:薛建珍一、追及与相遇问题1.相遇相遇的条件:两物体同一时刻到达同一位置。2.追及的特点:两物体一前一后的同向运动A追前方的B,设两者之间的距离Δs。若VAVB,则Δs;若VA=VB,则Δs。变大变小不变【例1】我国经济飞速发展,汽车走进了千家万户,驾车旅游成为一种休闲方式。在平直的公路上,一辆小汽车在路口等待交通灯,绿灯亮时在同一路口的一辆卡车以v0=10m/s的速度前进,小汽车立即以a1=2m/s2的加速度启动。请问小汽车启动后经过多长时间能追上卡车?此时汽车的速度为多大?讨论:在追及过程中,两车距离如何变化?当v1=v2时,两者具有最大的距离。【例2】一个步行者以6m/s的匀速跑步去追赶被红灯阻停的公共汽车,当他距离公共汽车30m时,绿灯亮了,汽车以1m/s2的加速度匀加速启动前进,问:人能否追上汽车?若能追上,则追车过程中人共跑了多少距离?若不能追上,人和车最小距离为多少?两者速度相等是判断能否追上的重要依据。假定A追B,若两者速度相等时:(1)A在B的后方,则,此时两者间的距离。(2)A在B的前方,则。(3)A、B在同一位置,则。追不上最小追上恰好追上,为临界状态二、追及相遇的解题思路及方法(1)画出两个物体运动示意图(2)理清两个关系:位移关系、时间关系(3)巧用一个条件:两者速度相等最值问题:两者速度相等时,出现最值。两个物体距离最大或距离最小。临界问题:两者到达同一位置,两者速度相同,则恰能追上或恰追不上(也是二者避免碰撞的临界条件)判天地之美,析万物之理!