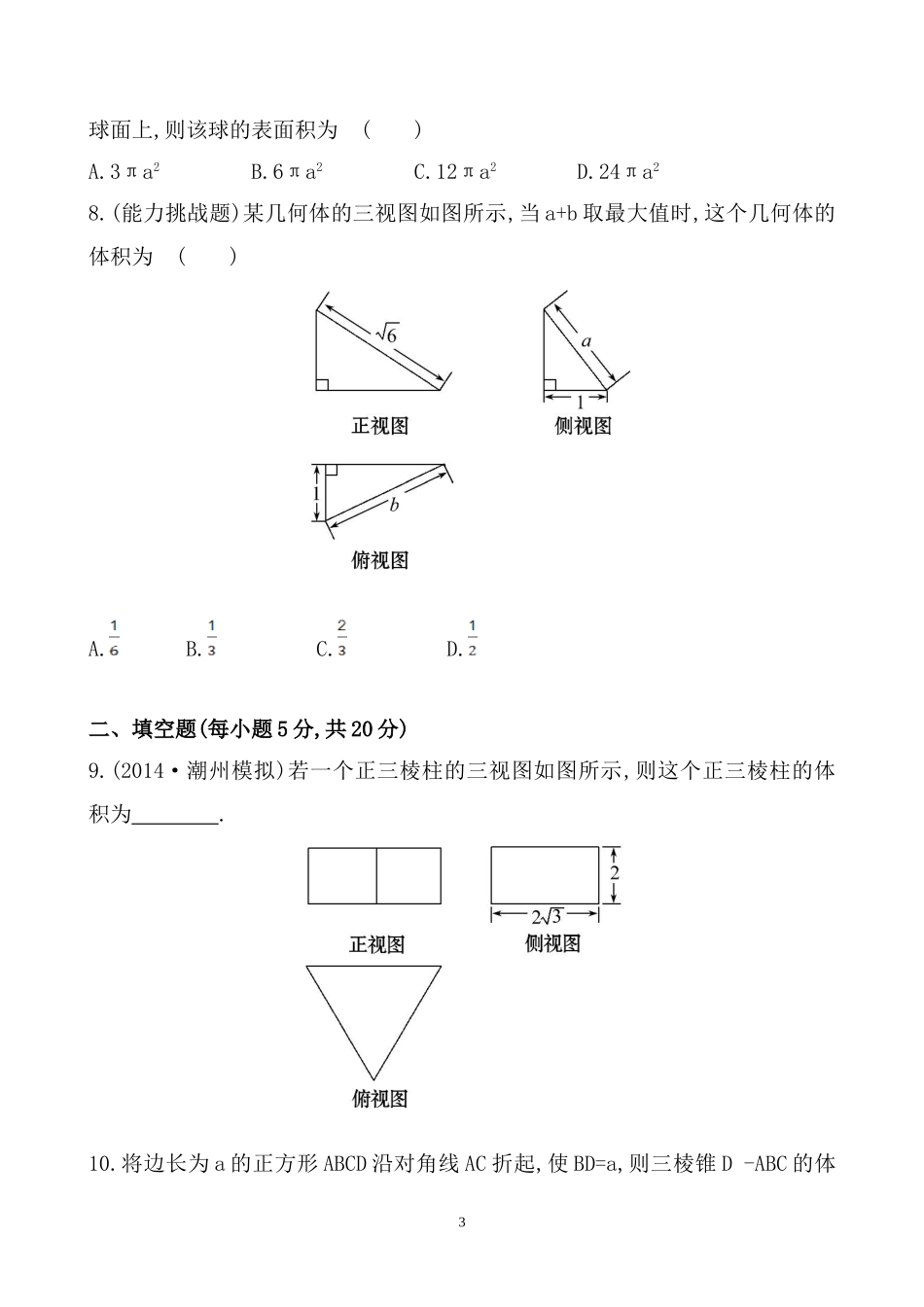
空间几何体的表面积与体积(45分钟100分)一、选择题(每小题5分,共40分)1.已知某球的体积大小等于其表面积大小,则此球的半径是()A.B.3C.4D.52.(2014·珠海模拟)轴截面为正方形的圆柱的侧面积与全面积的比是()A.1∶2B.2∶3C.1∶3D.1∶43.(2013·山东高考)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,该四棱锥侧面积和体积分别是()A.4,8B.4,C.4(+1),D.8,84.(2013·湖南高考)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于()1A.B.1C.D.5.(2014·揭阳模拟)一简单组合体的三视图及尺寸如图所示(单位:cm),则该组合体的体积为()A.72000cm3B.64000cm3C.56000cm3D.44000cm36.(2013·江西高考)一几何体的三视图如图所示,则该几何体的体积为()A.200+9πB.200+18πC.140+9πD.140+18π7.(2014·东北三校模拟)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个2球面上,则该球的表面积为()A.3πa2B.6πa2C.12πa2D.24πa28.(能力挑战题)某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为()A.B.C.D.二、填空题(每小题5分,共20分)9.(2014·潮州模拟)若一个正三棱柱的三视图如图所示,则这个正三棱柱的体积为.10.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体3积为.11.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.12.如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为cm3.三、解答题(13题12分,14~15题各14分)13.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形,(1)求该几何体的体积V.4(2)求该几何体侧面积S.14.如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:(1)该几何体的体积.(2)截面ABC的面积.15.(能力挑战题)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2.(1)求AB的长度.(2)求该长方体外接球的表面积.5答案解析1.【解析】选B.设球的半径为R,则πR3=4πR2,所以R=3.2.【解析】选B.设圆柱的底面半径为r,则圆柱的侧面积S侧=2πr·2r=4πr2,圆柱的全面积S全=2πr·2r+2πr2=6πr2,所以S侧∶S全=2∶3.3.【解析】选B.由图知,此棱锥高为2,底面正方形的边长为2,V=×2×2×2=,侧面积需要计算侧面三角形的高h==,S侧=4×=4.4.【解析】选D.根据条件得知正视图和侧视图一样,是正方体的一个对角面,故面积相等.5.【解析】选B.由三视图知,该组合体由两个直棱柱组合而成,故其体积V=60×40×10+20×40×50=64000(cm3).【加固训练】圆柱形容器内盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的半径是cm.【解析】设球半径为r,则由3V球+V水=V柱,6可得3×πr3+πr2×8=πr2×6r,解得r=4.答案:46.【思路点拨】先观察三视图得出几何体的结构特征,再代入体积公式进行计算.【解析】选A.由三视图知该几何体是一个组合体,上部是半圆柱,底面半径为3,高为2;下部为长方体,长、宽、高分别为10,4,5.所以此几何体的体积为π×32×2+10×4×5=200+9π.7.【解析】选B.由于长方体的长、宽、高分别为2a,a,a,则长方体的体对角线长为=a.又长方体外接球的直径2R等于长方体的体对角线,所以2R=a.所以S球=4πR2=6πa2.【加固训练】(2014·广州模拟)设一个球的表面积为S1,它的内接正方体的表面积为S2,则的值等于()A.B.C.D.【解析】选D.设正方体的棱长为a,则球的半径为R=a,所以===.8.【思路点拨】由三视图画出相应的直观图,然后构造出关于a,b的关系式,利用7基本不等式求最值.【解析】选D.由题意知,该几何体的直观图如图所示,且AC=,BD=1,BC=b,AB=a.设CD=x,AD=y,则x2+y2=6,x2+1=b2,y2+1=a2,消去x2,y2得a2+b2=8≥,所以a+b≤4,当且仅当a=b=2时等号成立,此时x=,y=,所以V=××1××=.【误区警示】解答本题常见的错误是忽视a+b取最大值这一条件.9.【解析】由侧视图知正三棱柱的高h=2,设正三棱柱的底...